Little Points of Light
Virtually everything we know about stars is based on spectroscopy, including what we know about magnitude, red shift, and why the night sky is dark.

"If people sat outside and looked at the stars every night, I'll bet they'd live a lot differently."
- Bill Watterson, creator of Calvin and Hobbes
In a column a few years ago about the solar spectrum (1), I mentioned that virtually everything we know about stars is based on spectroscopy. There are other spectroscopic aspects of stars besides their spectra. Here, I will present a few random thoughts about those little points of light in the sky.
Magnitude
One obvious aspect of stars is their perceived brightness: Some stars are brighter in the night sky than others. (We'll ignore the sun mostly in this installment.) In the second century BCE, the Greek astronomer and mathematician Hipparchus developed six categories of stars based on their apparent brightness, with each category termed a magnitude. Stars of the first magnitude were the brightest stars, while stars of the sixth magnitude were barely visible to the naked eye. Hipparchus cataloged approximately 1000 stars that were visible to him where he was, which was probably the island of Rhodes, off the coast of modern-day Turkey. Keep in mind that this was before the invention of the telescope and the concept of stellar distances had yet to be developed. Ptolemy popularized this scale in the second century CE.
In time, it was realized that the stars were various distances from the solar system. Given the inverse-square law that governs brightness, it was also understood that a dim star may be dim not because of its inherent brightness but because of its distance. Thus, we need to distinguish between the apparent magnitude (for which we use the symbol m) and the absolute magnitude (M). In 1856, English astronomer N. R. Pogson formalized the magnitude system by estimating that Hipparchus's first-magnitude stars were, on average, 100 times brighter than the sixth-magnitude stars. Revising the scale logarithmically, Pogson (2) defined a difference of one unit of magnitude as the fifth root of 100, or 5√100:
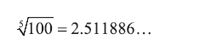
So, each unit of magnitude represented a brightness of about 2.5 more than the next-higher magnitude value. Because of how Hipparchus originally defined his rating system, the higher the magnitude, the dimmer the star. Very bright objects can actually have a negative magnitude.
However, we are still talking about an apparent magnitude, which is dependent on distance from the solar system. Astronomy defines an absolute magnitude as the magnitude of a star or galaxy as if it were at a distance of 10 parsecs from the observer. A parsec (which is a portmanteau of parallax and second and is defined as the distance that would yield a parallax of 1 arc second if the measuring baseline is one astronomical unit [AU], the average distance between the Earth and the Sun (for details, consult your friendly astronomy text) is 3.26 light-years, or about 3.08 × 1016 m, so 10 parsecs is 10 times that. In absolute terms, the magnitude M of the Sun is about 4.8, making it a rather dim star (sorry, sun worshippers, our sun is nothing special save that it's ours). In contrast, the star Rigel, the brightest star in the well-known constellation Orion, has an absolute magnitude of about –6.5, or more than 30,000 times as bright as the Sun. The equation relating the absolute magnitude M to the apparent magnitude m is:
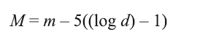
where d is the distance to the star. For stars that are very far away, relativistic corrections must be made to d, but we won't worry about that here. Note that this definition of absolute magnitude is good only for extrasolar objects like stars and galaxies. For planets and comets, a different definition of magnitude is used, based on a standard distance of 1 AU.
What we are calling brightness is more properly called luminosity, which is a measure of the amount of energy given off per unit time, has units of watts, and is, by definition, independent of distance. Visual luminosity is based on the visible portion of electromagnetic light, which can be problematic because some stars give off most of their energy in the infrared or even the ultraviolet region of the spectrum. The bolometric luminosity is a better measurement because it measures a star's output over a wider wavelength range.
Red Shift
One of the most profound ideas in science is based squarely on spectroscopy: The universe is expanding.
In 1842, Austrian physicist Christian Doppler proposed that the frequency of a wave is dependent on the relative velocities of the source and the observer. Curiously, Doppler's initial report was about the light coming from stars. In 1845, Dutch scientist C.H.D. Buys Ballot verified Doppler's prediction for sound waves, using calibrated musical notes being played on a passing train. This so-called Doppler effect is known to most people as the change in pitch made by passing trains, but it actually applies to all waves. For sound, the perceived frequency of the sound wave by a stationary observer is related to the frequency of the sound wave actually produced by a moving source by the equation
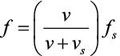
where f is the perceived frequency, fs is the frequency generated by the source, v is the normal velocity of the wave, and vs is the velocity of the source, considered positive if moving away from the observer and negative if moving toward the observer. (I am using f for frequency rather than the Greek letter nu to avoid confusion between nu and vee.)
In 1848, the Doppler effect was predicted again to be an effect on light by Hippolyte Fizeau, a French physicist. It was finally observed experimentally by British amateur astronomer William Huggins in 1868, who observed the shift in the Fraunhofer D line of the stellar spectra of various stars (3). By convention, if an object emitting light is moving toward the observer, frequencies are increased and the term blueshift is used. If the object emitting light is moving away from the observer, frequencies are decreased and the Doppler effect is called the redshift. In most (but not all) cases, astronomical measurements of spectra of extrasystem bodies like stars and galaxies involve redshift (more on this later.)
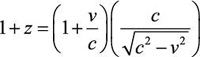
The modern formula for the velocity-related Doppler effect is where z is the Doppler shift, v is the velocity of the object with respect to the observer, and c is the speed of light. (I say "velocity-related" because there is also a redshift caused by gravitational fields. We are not considering those types of redshift here.) For nonrelativistic speeds, this reduces to

Figure 1: Spectra of a collection of galaxies showing the redshift in the spectrum. A velocity of 0.07 c corresponds to a z of 0.073. The shift in the absorption lines should be obvious and is larger at the red end of the spectrum, which is linear in wavelength, not frequency.
For low, nonrelativistic speeds, z << 1.0, but if the source speed is 60% of the speed of light relative to the observer, z is greater than 1 and approaches infinity as the velocity approaches the speed of light. Because of the accuracy in spectroscopic measurements, values of z corresponding to velocities on the order of meters per second are measurable. In fact, Mössbauer spectroscopy is essentially a measure of the red shift of gamma rays emitted from a nucleus, as this column recounted a few years ago (4).
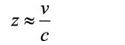
Now let's jump back to astronomy. For almost two centuries (since Fraunhofer in the 1810s) it has been understood that stars have spectra, either lines of light from the atoms emitting light or lines of darkness from atoms absorbing light. Almost all of the so-called Fraunhofer lines in the solar spectrum have been assigned to the spectroscopic transitions of various elements (the source of some of the lines remains in dispute to this day). Helium was first detected in the Sun in 1868 by English astronomer Norman Lockyer, 25 years before it was discovered on Earth. Buoyed by this success, later astronomers claimed detection of other new elements dubbed coronium and nebulium after their cosmic sources, but later work identified these "new" elements as already-known atoms. Astronomic spectroscopic study was also applied to those misty objects called nebulae (singular nebula), named from the Latin word for "cloud" because of their indistinct appearance in earlier telescopes.
During a study of nebulae in 1912, American astronomer Vesto Slipher discovered that the nebula called Andromeda had Fraunhofer spectral lines in the blue and violet regions of the visible spectrum that were actually blueshifted, indicating a relative velocity of 300 km/s toward us (5). This corresponds to a z value of –0.001, according to the equation above.
In the early 1920s, American astronomer Edwin Hubble noted a type of variable star in several nebulae, including Andromeda, demonstrating that they are not misty objects, but galaxies in their own right. Thus, astronomical spectroscopy was re-defined as measuring the spectra of galaxies, not just stars. Figure 1 shows the redshifting of a spectrum of a group of galaxies; note how the pattern of absorption shifts, due to the relative velocity of the light source.
Measuring the spectra of galaxies, Hubble and his colleagues noted some interesting data: With only a few exceptions (the Andromeda galaxy is one), all galaxies' spectra showed a redshift. Furthermore, they also noted a rough correlation: The greater the estimated distance of a galaxy, the greater its redshift, and thus the faster it is moving away from us. Therefore, the universe is expanding. In 1929, Hubble and his colleague Milton Humason announced what is now known simply as Hubble's law: The farther away a galaxy is, the faster it is receding from us. Simply put, Hubble's law is
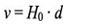
where v is the velocity of the galaxy, d is its distance from us, and H0 is called the Hubble constant. The value of the Hubble constant is of immense value to understanding the overall nature of the universe. Current estimates put the value of H0 at 70.6 ± 3.1 kilometers per second per megaparsec (1 megaparsec = 1,000,000 parsecs or 3,260,000 light years or 3.08 × 1022 m), expressed as 70.6 km/s/Mpc.
All this from spectroscopy.
Why is the Night Sky Dark?
Imagine, at first approximation, an infinite, static universe with stars equally distributed, on average, throughout space. (There can be local variations, but in general this is a good assumption.) If you were to go outside at night and look in any direction, eventually your line of sight should end on a star. That star would be shining and contributing some number of photons to the overall picture of the night sky.
Why isn't the night sky bright, then? In fact, it should be infinitely bright. Put another way, Why is the night sky dark? If our assumptions are correct, the night sky shouldn't be dark. But it is, and the fact that it is so is called Olbers' paradox, after German astronomer Heinrich Olbers, who stated it in 1823 (although it may have been stated originally as early as the late 1500s).
No satisfactory reasons for this phenomenon were proposed until Hubble's work on galactic redshifts. If all galaxies are moving away from us, then turn the clock back: At some point in the past, all galaxies should have started from the same point and then started to move outward. By studying the redshifts and velocities of many galaxies, astronomers postulate that the point of ultimate galactic coalescence was about 13.7 billion years ago; the event that started galaxies moving apart is unceremoniously called the Big Bang, and its occurrence is currently the leading paradigm in modern cosmology. Because light is the fastest known phenomenon, the entire universe is about 13.7 billion light years in radius. That may be large, but it isn't infinitely large. Thus, one of the assumptions of Olbers' paradox is incorrect: The universe is not infinite; rather, it is finite, and there are many directions you can look without looking at a star (or galaxy).
Some argue that this merely shifts the issue. At any direction, we should eventually see a remnant of the Big Bang, which was undoubtedly hotter and brighter than a star. Why isn't the night sky infinitely hot and bright? The standard answer to that is redshifting. When light is redshifted, not only is its frequency reduced, but — according to Planck's quantization law — so is its energy. The farther away a light source is, the faster it is traveling with respect to us and the more its energy has shifted down. Thus, the total amount of light intercepted by us from the universe around us is finite and less energetic than it could be. As a result, the night sky is dark.
And all this from the spectroscopy of those little points of light.

David W. Ball David W. Ball is a professor of chemistry at Cleveland State University in Ohio. Many of his "Baseline" columns have been reprinted in book form by SPIE Press as The Basics of Spectroscopy, available through the SPIE Web Bookstore at www.spie.org. His book Field Guide to Spectroscopy was published in May 2006 and is available from SPIE Press. He can be reached at d.ball@csuohio.edu his website is academic.csuohio.edu/ball.
References
(1) D.W. Ball, Spectroscopy 20 (6), 30–31, (2005).
(2) N.R. Pogson, Monthly Notices of the Royal Astronomical Society 17, 12–15 (1856).
(3) W. Huggins, Phil. Trans. Royal Soc. London 158, 529 (1868).
(4) D.W. Ball, Spectroscopy 18 (2), 70–72 (2003).
(5) V. Slipher, Bull. Lowell Observ. 1, 56–57 (1912).

Cancer Diagnosis: New Raman Spectroscopy Method Eliminates Fluorescence Interference
January 21st 2025Researchers from Tsinghua University have developed an innovative dual-wavelength Raman spectroscopy method that eliminates fluorescence interference in measuring esophageal tissue samples. This development enables precise identification of molecular changes in these tissues, with potential applications in early esophageal cancer diagnosis.
Raman Spectroscopy to Detect Lung Cancer and Monitor Vaccine Effects
January 20th 2025A new study highlights the use of Raman spectroscopy to detect lung cancer and evaluate the effects of the PCV13 vaccine. Researchers found distinct biochemical changes in lung cancer patients and healthy individuals, revealing the vaccine's significant impact on immune response.
Nanometer-Scale Studies Using Tip Enhanced Raman Spectroscopy
February 8th 2013Volker Deckert, the winner of the 2013 Charles Mann Award, is advancing the use of tip enhanced Raman spectroscopy (TERS) to push the lateral resolution of vibrational spectroscopy well below the Abbe limit, to achieve single-molecule sensitivity. Because the tip can be moved with sub-nanometer precision, structural information with unmatched spatial resolution can be achieved without the need of specific labels.
An Inside Look at the Fundamentals and Principles of Two-Dimensional Correlation Spectroscopy
January 17th 2025Spectroscopy recently sat down with Isao Noda of the University of Delaware and Young Mee Jung of Kangwon National University to talk about the principles of two-dimensional correlation spectroscopy (2D-COS) and its key applications.