Group Theory and Symmetry, Part I: Symmetry Elements

Symmetry is one of those things that people recognize but is hard to define. For example, most people recognize that a square is more symmetric than a rectangle, but they would have a difficult time defining why a square is more symmetric than a rectangle.

For our purposes, symmetry can be defined as a sort of shape similarity. A square is more symmetric than a rectangle because all four of its sides are equal, whereas in a rectangle, only two sides are equal.

David W. Ball

However, the mathematical treatment of symmetry has more to it than that. There are certain specific operations that can be performed on an object to reorient that object in space, and if the exact same-looking shape is generated, the object has symmetry. The more of these sorts of operations that can be performed to regenerate the exact same shape in space, the "higher" the symmetry of the object. Here, we will introduce the different operations that are used to define the symmetry of an object.

Rotational Symmetry

Consider the square in Figure 1. One of the corners has been marked by an asterisk. If we rotate the square by 90°, note that the asterisk moves position but the square remains looking like, well, a square. The resulting square looks exactly like the initial square. Consider, however, the rectangle in Figure 1. When it is rotated by 90°, it is still the same rectangle to be sure, but now it is oriented differently. It is not the same-looking rectangle in space that we started with. We say, then, that the square has a rotational axis of symmetry that the rectangle doesn't. In this case, the symmetry axis would be going through the center of the square, right through the plane of the printed paper. Because we turned the square by one fourth of a full circle, we say that the square has a fourfold rotational axis of symmetry. (Axes of symmetry are named for the number of times an object has to rotate to return to its original starting position; in this case, the square would be rotated four times to return to its starting position.) The rectangle has a twofold axis of symmetry, because we can rotate the rectangle by one half of a circle, 180° and generate a similar-looking rectangle in the same orientation.

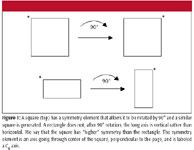
Figure 1

A rotational axis of symmetry is one type of symmetry element. The actual performance of the rotation by the object is called a symmetry operation. An object is said to "have a symmetry element" if the operation performed by the symmetry element yields a new shape that is oriented exactly like the original shape is oriented, even though the parts of the shape have moved. Rotational axes of symmetry are labeled as C_n, with the n standing for the 1/nth of a circle the object is rotated. Hence, the square has a C₄ axis of symmetry going through its center, while the rectangle does not. The square is said to have a "fourfold" axis of symmetry, and the value of four is called the order of the axis.

An object can have more than one of the same type of symmetry element. For instance, coincident with the C₄ axis of the square is also a C₂ axis, because you can also rotate a square by one half of a circle and get the same square back. The C₂ can be thought of as performing a C₄-type of rotation twice, but the C₂ symmetry element is in fact a unique symmetry element. The square also has some other C₂ axes, as shown in Figure 2. The rectangle shares some of these axes, but not others. It is partly because of this that the square is considered higher symmetry than the rectangle — it has more symmetry elements.

Figure 2

Reflection Symmetry

Another type of symmetry element is the reflection plane, which is symbolized by the lowercase Greek letter sigma α. This symmetry element is exactly what it sounds like: a plane that acts as a mirror, reflecting all points of a shape to the other side of the mirror. If the exact same shape oriented in space is produced, the object is said to have a reflection plane of symmetry.

Figure 3 demonstrates a reflection plane of symmetry. The pentagon on top is split by a mirror that goes through the plane of the page. As is demonstrated by the indicated point, if that point is reflected to the other side of the plane, it falls back on the pentagon shape. Reflecting all points on the pentagon will end up reproducing the original pentagon, so this pentagon has a reflection plane of symmetry as a symmetry element. However, the crescent on the bottom does not have the indicated plane of symmetry, because reflecting all points on the crescent through the plane would not regenerate the original shape. In this regard, the crescent is acting like your hands — they are reflections of each other, but not the same orientation in space. (You can verify this by putting your hands on a table palm-down and trying to superimpose your thumbs and pinkies — you won't be able to!) Note that the plane of the page also forms a reflection plane of symmetry for both shapes in Figure 3. Each point on the shape is reflected on itself.

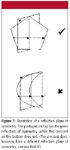
Figure 3

Reflection planes are classified by whether or not they contain the rotational axis of highest order, the so-called principal axis. If a reflection plane contains the principal axis, it is called a vertical plane of symmetry and given the symbol α_v. There can be more than one vertical plane of symmetry in an object. If the reflection plane of symmetry is perpendicular to the principal axis, it is called a horizontal plane of symmetry and given the symbol α_h. If a shape has a horizontal plane of symmetry, it has only one; you cannot have more than one horizontal plane of symmetry in an object. As it is conventional to orient an object to put the principal axis in an up-and-down orientation, these descriptions of reflection planes make sense.

Some shapes have vertical planes that bisect two different C₂ axes. If this is the case, these vertical planes are called dihedral planes, and are given the symbol α_d. However, dihedral planes are just another type of vertical plane.

Identity and Center of Inversion

Likely the most simple symmetry element is identity, represented by E (from the German word "einheit", meaning unity). Identity is the symmetry element of existence; all objects have this symmetry element, even if they have no other symmetry element. This begs the question, then: Why is this symmetry element even necessary? The answer is that it's necessary because of the mathematical requirements of group theory. Just like the number zero is an important part of arithmetic, so is identity important in group theory and symmetry.

The next symmetry element is the center of inversion, symbolized by i. This symmetry operation is a reflection through a point at the center of an object in the same direction and at the same angle. Figure 4 shows a shape that has a center of inversion and a shape that does not. As its name implies, if an object does have a center of inversion symmetry element, the point that everything is reflected through is in the center of the object.

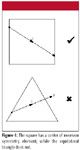
Figure 4

Improper Rotation

The last symmetry element we will consider is the most unusual. It is called an improper axis of rotation, and is denoted S_n. It is a rotation by 1/nth of a circle followed by reflection through a plane that is perpendicular to the rotational axis. Figure 5 demonstrates the improper rotational axis. The scroll is rotated by 180° about an axis, and then reflected through a plane that is perpendicular to that axis. Note that the original shape in space is reproduced, so this scroll has an S₂ symmetry element.

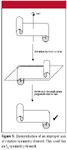
Figure 5

Improper axes of rotation can be notoriously difficult to find or visualize. Why, then, are they necessary? For the same reason that identity is defined as a symmetry element: the mathematical properties of groups require them.

Point Groups

As it turns out, not every random combination of symmetry elements exist for any real object. In fact, only certain combinations of symmetry elements are possible for any real three-dimensional object. These combinations are called point groups. They are called this because all of the symmetry elements of the shape will intersect at (at least) a point. While technically there are an infinite number of point groups (for example, a rotational axis can have any number as its order), only a few are scientifically relevant. For example, in crystallography, it has been demonstrated that there are only 32 different ways that a crystal can fill three-dimensional space (this is known as the crystallographic restriction theorem and applies to true crystals, not quasicrystals).

Consider the arch in Figure 6. It has four, and only four, symmetry elements, which are superimposed on the arch: it has the E identity element, a C₂ axis of rotation, and two different planes of reflection (one of which is arbitrarily labeled with a prime). That's all, nothing else. These four symmetry elements constitute a mathematical group labeled C_2v (spoken as "sea-two-vee"). By virtue of having this point group, this shape will have certain physical properties.

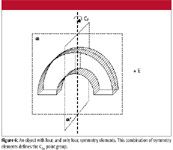
Figure 7

How does this apply to spectroscopy? Well, molecules have shapes too. Consider Figure 7. It is the same as Figure 6 but has a water molecule drawn instead of an arch. See how the water molecule has the same symmetry elements as the arch does? As such, it has the same symmetry point group: C_2v. Because of this, the water molecule will have certain properties that it shares with the arch. For example, the electrons in the water molecule are imbalanced in such a way that the molecule has a dipole moment. If the arch in Figure 6 were composed of electron density, it too, would have a dipole moment. Because the shape of the molecule is dictated by electronic wavefunctions, it should come as no surprise that the wavefunctions will have C_2v symmetry as well. Spectroscopy is the interaction of light with wavefunctions, so symmetry ultimately becomes very important in spectroscopy. But we have a ways to go before we can consider wavefunctions.

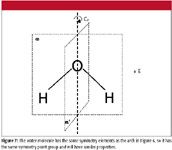
Figure 8

In our next installment, we will find out what a mathematical group is and how these symmetry elements do indeed satisfy the definition of a group. Stay tuned

David W. Ball is a professor of chemistry at Cleveland State University in Ohio. Many of his "Baseline" columns have been reprinted in book form by SPIE Press as The Basics of Spectroscopy, available through the SPIE Web Bookstore at www.spie.org. Another book, Field Guide to Spectroscopy (published in May 2006), is available from SPIE Press. He can be reached at d.ball@csuohio.edu his website is academic.csuohio.edu/ball.