The Nature and Utility of Mass Spectra

The phenomenal growth of mass spectrometry (MS) as a diverse analytical tool, especially when viewed from my occasional role teaching and participating in liquid chromatography–mass spectrometry (LC–MS) courses, has underscored the need for useful references: courses, books and various learning tools. Unfortunately for some who seek to expand their knowledge of the field, a well-meaning purveyor of knowledge may unwittingly assume the student understands more than they actually do. In a recent interview, Professor Harold McNair, renowned for his book Basic GC, describes the book's genesis, which harkens back to a 1963 lecture he gave at the University of Athens, Greece. After that first lecture, he says, the faculty begged him to return the following day. After four lectures, they begged him to commit the lectures to paper. Hence, the initial draft of Basic GC. Written for Europeans for whom English is a second language, the book adopts a basic English style. "It was a simple book," says McNair, "easy to read." Eventually translated into eight languages, the book sold over 130,000 copies (1). Hence, by happenstance, a sorely needed text became the basis for training at universities and the model for short courses.

Almost a half-century later, we enjoy far greater access to the experience of others via the internet. This month's column addresses some elementary aspects of the mass spectrum, discusses tools employed by experienced practitioners, and provides some glimpses into current advances in the science and art of deriving unambiguous answers from unknown spectra.

Basics of the Mass Spectrum

The sine qua non for practitioners is, of course, mastery of the language of MS, which takes the form of spectral output. Jim Clark, a retired chemistry teacher in the U.K., has developed an accessible, comprehensive, and useful resource that captures a wealth of experience from his years teaching. His Web site (www.chemguide.co.uk), aimed more at beginning students than advanced ones, serves as a quick refresher for the scientist–practitioner who does not regularly use MS. Many of the examples in the first section of this column are adapted from Clark's work updated with our current appreciation of accurate mass and atmospheric pressure ionization practice. Take from it what you will and apply as needed.

Tools of the Experienced Practitioner

We have seen various software tools used to search for an unambiguous answer to what a spectrum represents. James Little (http://users.chartertn.net/slittle) provides some insight to using the tools and how he approaches problem solving.

Deriving the Unambiguous Answer

Defining the unique qualities of the spectrum gives us a basis for de novo assessments. As comfortable as we can be with the fidelity of isotope prediction, it does not mean we can apply rules to flawlessly derive the only possible unambiguous formula from an acquired ion. Kirsten Hobby (see http://kisotopic.com) worked to develop a software tool (referred to as iFit in MassLynx software, Waters Corp., Milford, Massachusetts) to compare an acquired spectrum with its theoretical equivalent. Hobby's comments from a few years ago on the limits and utility of what he designed to help derive an answer are compared with thoughts from Richard Denny, current architect of MassLynx spectral "fitting" tools.

The Molecular Ion (M⁺) Peak

The formation of molecular ions: In common applications of electron ionization (EI), a flash-vaporized organic sample passes into the ionization chamber to encounter a stream of 70-eV electrons. These electrons are highly energetic, enough so to snatch an electron from the outer shell of an organic molecule. In so doing, they form a positive ion (radical cation), a molecular ion. When ionization occurs in atmospheric techniques like electrospray ionization (ESI) — albeit by very different mechanisms — this ion is called the pseudomolecular ion (M+H) after forming by adding a proton (rather than extracting an electron). The resulting ion can also be referred to as the parent ion or, in more modern usage, the precursor ion, when the ion is the first step in a fragmentation experiment such as MS-MS.

The molecular ion is often given the symbol M.⁺. Note the dot beneath the "+," which signifies that somewhere in the ion, a single, unpaired electron remains from what was originally a pair of electrons. (The other half of the electron pair was removed in the ionization process.) Because of the high level of energy imparted in EI, the molecular ions tend to be unstable. Some bonds break, producing additional fragment ions. In an MS spectrum, ions including those fragments are often represented as the centroid of each ion peak. Losing the additional "envelope information" shown in the original profile or continuum peak of the MS ion current to produce the familiar stick-plot representation of a spectrum also saves data storage and enhances address speed.

The simplest example is a molecular ion that breaks into two parts. One part is another positive ion, the other an uncharged free radical.

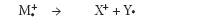
An uncharged free radical does not produce a line on the mass spectrum. Only charged particles are accelerated, deflected, and detected by the mass spectrometer. Uncharged particles simply become lost in the instrument, eventually getting removed by the vacuum pump.

The ion X⁺ travels through the mass spectrometer just like any other positive ion. It produces a line on the stick diagram.

In the mass spectrum, the heaviest ion (the one with the greatest m/z value farthest to the right) is likely the molecular ion. The mass spectra of a few compounds do not contain a molecular ion peak, because all the molecular ions break into fragments, which is rarely the case with atmospheric "soft" ionization techniques like ESI. The spectral result is a statistical outcome for a very large population of molecules undergoing ionization. Not all fare alike, depending upon various factors including the source design itself. For example, in the mass spectrum of pentane, the heaviest ion has a mass-to-charge (m/z) value of 72 (Figure 1). Unlike in ESI, the energy causing ionization is not conserved, so the molecular ion is quite small compared with the resulting fragments.

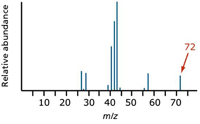
Figure 1: Simplified mass spectrum of pentane. The largest m/z value, 72, represents the largest ion going through the mass spectrometer.

Practitioners find the molecular ion's presence in an unambiguous spectrum reassuring, for the task of assigning the relative formula mass from a mass spectrum then becomes trivial. They simply look for the peak with the highest m/z value. That value is the relative-formula mass of the compound. Nevertheless, complications can arise because of the possibility of different isotopes (carbon, M+1, or chlorine/bromine, M+2, patterns) in the molecular ion. You may see these referred to as "A+1" and "A+2" elements as well but we will use the designation "M" here.

Accurate isotopic masses: For normal calculation purposes we round off relative isotopic masses: ¹H = 1, ¹²C = 12, ¹⁶O = 16, and so forth.

Accuracy to four decimal places is common for use in high resolution/accurate mass work, however and we need to consider ¹H = 1.0078, ¹²C = 12.0000, ¹⁶O = 15.9949.

The carbon value is 12.0000, of course, because all the other masses are measured on the carbon-12 scale (based on the carbon-12 isotope, the mass of which is exactly 12).

Using accurate values to find a molecular formula: Two simple organic compounds have a relative-formula mass of 44: propane, C₃H₈, and acetyldehyde, CH₃CHO. Using accurate mass the molecular ion peaks for the two compounds give the following mass-to-charge values: C₃H₈ = 44.0621 and CH₃CHO = 44.0257.

To illustrate, a gas known to contain only the following isotopes produces a molecular ion peak at m/z 28.0308. Using nominal mass (approximately 28), you can predict three structures that contain the elements from the list: N₂, CO, and C₂H₄. Working with accurate molecular ion masses for these gives N₂ = 22.0056, CO = 27.9944, and C₂H₄ = 28.0308. The gas is obviously C₂H₄.

In "real life," trying to work out all the possible things that could add up to the value you want is quite time-consuming. It's easy to see how this exercise contains errors even when measuring low masses, where mass accuracy is at its best!

The M+1 Peak

The carbon-13 isotope: The presence of the carbon-13 isotope in the molecule produces the M+1 peak. Do not confuse it with the less common, radioactive, carbon-14 isotope. A stable isotope of carbon, ¹³C makes up 1.07% of all carbon atoms by the current IUPAC recommendation (8). We often conveniently consider the naturally occurring abundance to be 1%.

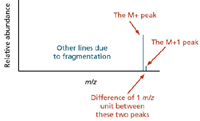
Figure 2: The small peak or line one unit to the right of the main or molecular ion peak is called the M+1 peak.

Consider methane (CH₄). Approximately 1 in every 100 methane molecules contains carbon-13 rather than the more common carbon-12. So 1 in every 100 methane molecules has a mass of 17 (13 + 4) rather than 16 (12 + 4). Thus the mass spectrum for methane includes a line corresponding to the molecular ion (¹³CH₄).⁺ as well as one to (¹²CH₄).⁺. Moreover, the line at m/z 17 is much smaller than that at m/z 16 because the carbon-13 isotope occurs far less frequently. Statistically, a ratio of approxmately 1 of the heavier ions occurs for every 99 of the lighter ones.

What happens when there is more than one carbon atom in the compound?: Imagine a compound containing two carbon atoms. Either of them has an approximately 1-in-100 chance of being ¹³C (Figure 3). So a 2-in-100 chance exists for the molecule as a whole to contain one ¹³C atom rather than a ¹²C atom, which leaves a 98-in-100 chance of both atoms being ¹²C. The corresponding ratio of the height of the M+1 peak to the M peak is therefore 2:98, which gives an M+1 peak of approximately 2% the height of the M peak.

Figure 3: Spectral distribution of naturally occurring ions.

Small numbers of carbon atoms: Measuring the height of the M+1 peak as a percentage of the height of the M peak yields the number of carbon atoms in a compound. We have seen that a compound with two carbons gives an M+1 peak of approximately 2% the height of the M peak. Similarly, you could show that a three-carbon compound gives an M+1 peak of about 3% of the height of the M peak.

Larger numbers of carbon atoms: The approximations we are making won't hold given more than two or three carbons. This is often a troubling concept for students. The proportion of carbon atoms that are ¹³ C isn't 1%. And the approximation that a ratio of 2:98 is about 2% does not hold as the small number increases. A quick look at high resolution spectra of compounds containing hundreds of C will show the ¹² C no longer dominates and at low resolution (where the fine isotopic features are lost) the peak top shifts. The way we define the molecule of interest can exert a profound effect on our search results (see the MS Primer on definitions www.Waters.com under "Education & Events – Primers" in the section "Mass Accuracy and Resolution").

A colleague in Manchester, United Kingdom, Richard Denny, currently the architect for software using isotope characteristics to improve our analytical results points out "Assuming 1.07% is an appropriate value for the sample under consideration and that the only element contributing to M+1 is carbon, a rule of thumb directly derived from the binomial distribution is n = r(100-p)/p, where r is the observed ratio (M+1)/M, n is the number of carbons, and p is the percent ¹³C isotope abundance. If the assumptions pertain and the measured values are accurate, this rule should be good for a larger number of carbons. The problem is that measurement errors, possible contributions to the M+1 from other elements and the correctness of the assumed ¹³C ratio come in to play, particularly at higher masses."

The mass spectrum of monatomic elements: Monatomic elements include all except those like chlorine (Cl₂), whose molecules include more than one atom. The two peaks in a mass spectrum of boron show two isotopes with relative isotopic masses of 10 and 11 on the ¹³C scale. Isotopes are atoms of the same element; they therefore have the same number of protons. Their masses differ however, as a result of unequal numbers of neutrons. Assume here that all the ions recorded have a charge of 1+ (m/z gives you the mass of the isotope directly). According to the carbon-12 scale, the mass of the ¹²C isotope weighs exactly 12 units.

The abundance of isotopes: With the caveats already discussed in place, the relative size of each peak gives you a measure of the relative abundances of the isotopes. The tallest peak (base peak) is often assigned an arbitrary height of 100, but you can use any scale.

In this case, the two isotopes (with their relative abundances) are boron-10 = 23 and boron-11 = 100.

Relative atomic mass: The relative atomic mass (RAM) of an element is given the symbol Ar and is defined as the weighted average of the masses of the isotopes relative to 1/12 of the mass of a carbon-12 atom.

A "weighted average" allows for the fact that the amounts of the various isotopes are unequal.

Example: Of 123 atoms of boron, 23 would be ¹⁰B, and 100 would be ¹¹B. Thus the total mass would be (23 = 10) + (100 × 11) = 1330

The average mass of these 123 atoms would be 1330 + 123 = 10.8 (to three significant figures). The relative atomic mass of boron is 10.8.

Notice the effect of the weighted average. A simple average of 10 and 11 is, of course, 10.5. Our answer of 10.8 allows that many more of the heavier isotope of boron exist, giving a more accurate weighted average.

Some Examples

The number of isotopes: The five peaks in the mass spectrum show five isotopes of zirconium (Figure 4), with relative isotopic masses of 90, 91, 92, 94, and 96 on the ¹²C scale, the relative abundances are given as percentages.

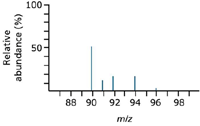
Figure 4: A typical mass spectrum for zirconium.

The five-isotope relative abundance (percentages):

Zirconium-90 51.5

Zirconium-91 11.2

Zirconium-92 17.1

Zirconium-94 17.4

Zirconium-96 2.8

Assume for every 100 atoms of zirconium, 51.5 would be ⁹⁰Zr, 11.2 would be ⁹¹Zr, and so forth.

The total mass of these 100 typical atoms would be (51.5 × 90) + (11.2 × 91) + (17.1 × 92) + (17.4 × 94) + (2.8 × 96) = 9131.8

The average mass of these 100 atoms would be 9131.8 + 100 = 91.3 (to 3 significant figures).

The relative atomic mass of zirconium is 91.3.

The mass spectrum of chlorine: Chlorine has two isotopes, ³⁵Cl and ³⁷Cl, in the approximate ratio of three atoms of ³⁵Cl to one atom of ³⁷Cl. If the rules presented so far hold true, the mass spectrum would look like the one shown in Figure 5.

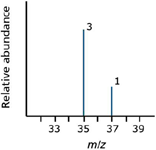
Figure 5: A typical mass spectrum of chlorine.

But chlorine consists of molecules, not individual atoms. When it is ionized by EI, an electron is knocked off the molecule to give a molecular ion, Cl₂⁺. These molecular ions are not particularly stable; some fragment to give a chlorine radical and a Cl⁺ ion.

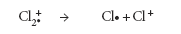
The Cl.⁺ ions pass through the instrument and give lines at 35 and 37, depending on the isotope, and would produce exactly the pattern as in the last diagram. The problem is that you will also record lines for the unfragmented Cl₂.⁺ ions.

Thinking about the possible combinations of chlorine-35 and chlorine-37 atoms in a Cl₂⁺ ion, you realize that both atoms could be ³⁵Cl, both could be ³⁷Cl, or one of each could pair. That would give these total masses for the Cl₂⁺ ion:

35 + 35 = 70

35 + 37 = 72

37 + 37 = 74

Thus a set of lines in the m/z 70 region would look like the spectrum shown in Figure 6. The relative heights of the 70, 72, and 74 lines are in the ratio 9:6:1.

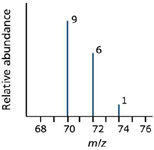
Figure 6: Added spectral complexity of chlorine. These lines would be in addition to the lines at 35 and 37.

You cannot predict the relative "heights" or abundances of the lines at 35/37 compared with those at 70/72/74. Doing so would depend on the proportion of molecular ions breaking up into fragments, which you cannot know. The overall mass spectrum looks like the spectrum shown in Figure 7.

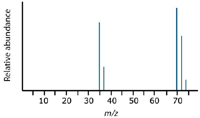
Figure 7: Complete theoretical chlorine spectrum.

Instrumental errors: Although practices have evolved significantly, along with software tools, an example posted on the Scripps website (http://fields.scripps.edu/sequest/information.html) from some years ago illustrates the point.

The software in the cited illustration notes that, by default, the mass is set to monoisotopic. Yet when the instrument software selects a peak from the MS scan to perform MS-MS on, there's no guarantee that it is always selecting the ¹²C isotope peak versus the ¹³C isotope peak as the precursor mass. As the authors note, "zooming in" on the MS scans shows that the "isotope" peaks differ in mass from 0.7 to over 1.0 amu for doubly and triply charged peptides, diminishing the ability to label the peaks as "isotope peaks." What this means is that (especially for larger peptides) the (M+H)⁺ mass calculated in each file is inaccurate by a factor of 1–3 amu (or more):

"(I)t might be better to search with a large mass tolerance, or use average masses to compensate a bit for the wrong (larger) precursor peak mass being selected. Our lab has always performed database searches using average masses, since the peptide mass error is better than with monoisotopic masses . . . the above 'isotope' error could explain why this would be the case."

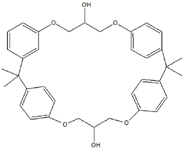
Figure 8: Unknown identified as can extract - cyclo-DiBADGE, C36H40O6.

Notes from the experienced practitioner: James Little and colleagues at Eastman Chemical Company (Kingsport, Tennessee) posted similar discussions based upon years of effort for the benefit of the rest of us. Their laboratory makes use of gas chromatography (GC)–MS and LC–MS. Much of the work involves identifying unknowns in samples for which knowledge is easily accessed. Yet they are also confronted with challenges where they lack sample history in the characterization of competitive samples.

Little says the GC–MS work is much more straightforward, the result of computer searchable EI databases. His group currently searches a database consisting of 1,055,524 entries, with 50,000+ being in its proprietary corporate database.

LC–MS analyses, however, are somewhat more complicated, though they are fairly successful employing several different approaches. They often inject things both derivatized (BSTFA, methyl esters) and underivatized by GC–MS. Little says that what one can get to elute from a GC column is surprising. Accurate mass data, in-source CID, and isotope matching normally allows determination of the molecular formulas for most components from LC–MS analyses.

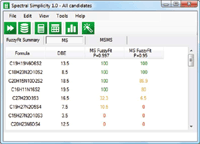
Figure 9: Step 1: Generate MS data. 99.7 and 95% confidence limits.

Little uses the list of 64,000+ compounds available through the Toxic Substances Control Act (TSCA), available in various forms, to search by molecular formula, nominal mass and exact monoisotopic accurate mass (see more detail at http://users.chartertn.net/slittle/tsca.html). He says the modified search available at his site is handy because he corrected all of the molecular weights for the free base or acid for charged species.

Little also reports ChemSpider (www.chemspider.com), a free online source of structure-based chemical information, to be very useful. He says that normally, by molecular formula or monoisotopic accurate mass using the additional "Filter only those having patents" link, he usually knows he is looking for something with certain properties (UV stabilizer, antioxidant, optical films, and so forth). So seeing the patent usually tells him he is going down the correct path.

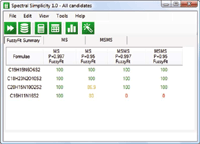
Figue 10: Step 2: Add MS-MS data - fourth candidate eliminated.

SciFinder (www.cas.org), an online, graphical interface for searching the Chemical Abstracts Service (CAS) databases, is a subscription service that works extremely well for Little's group. As with many search engines, typing in the molecular formula produces a candidate list. For example, searching based on the limited detail of an extract from a can coating with a tentative formula of C₃₆H₄₀O₆ produces, according to Little, "a lot to look through" (140 entries). Instead of looking at structures, he selects the "Get References" option to show only the analytical ones, which generates a list showing things that migrate from cans.

Little has also developed a very successful approach for identifying surfactants using a residual MW calculation http://users.chartertn.net/slittle/surfactants.html

Little computer searches LC–MS-MS spectra of unknowns against a database of 17,000 MS-MS spectra composed of true hybrid instrument spectra and in-source CID. He says this approach works reasonably well but his success is limited as compared to electron ionization spectra searches due to the limited size and quality of the available MS-MS databases. He hopes that one day someone will discover a way to generate somewhat useful "in-silica" spectra from the large collection of structural databases available from sources such as Chemspider and CAS Registry.

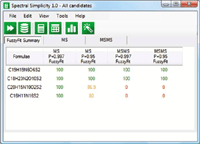
Figure 11: Step 3: Apply known fragmentation relationships - third candidate eliminated.

Looking forward to an unambiguous answer: The high mass accuracy provided by the quadrupole time-of-flight (QTOF) system, whose resolution can be 10 times higher than a quadrupole's and whose mass accuracy falls within a few parts per million of the true calculated monoisotopic value, makes empirical formula determination based on mass defect possible (where the critical mass value of hydrogen is a differentiator).

Determining the difference for instance, between an aldehyde and a sulfide, could be accomplished with an increase in mass accuracy above typical quadrupole limits, to 30 ppm, where the two differ by 0.035 Da. Consider the metabolic processes of methylation (addition of CH₂), which produces an increase over the precursor (response for the drug alone) in the measured mass on the instrument of +14.0157, as opposed to a two-stage biotransformation involving hydroxylation (addition of oxygen) followed by oxidation at a double bond (loss of H₂), which produces an increase of +13.9792. Both measurements, when limited by nominal resolution typical of quadrupole response, look like +14.

The requirements for unambiguous characterization from the Journal of the American Society for Mass Spectrometry author's guidelines (March 2004) establish, for C, H, O, N compositions where C_0–100, H_3–74, O_0–4, and N_0–4, a nominal m/z response at 118 needs only an error not exceeding 34 ppm to be unambiguous, where an m/z response at 750 requires precision greater than 0.018 ppm to eliminate "all extraneous possibilities."

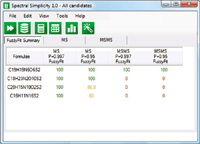
Figure 12: If you assume that the first fragment was formed by the loss of a neutral species, which is quite likely, then only the correct formula remains.

A number of recently introduced tools such as Waters' i-FIT algorithm and Element Prediction algorithm, Applied Biosystems' Formula Finder (2), and Bruker's Sigmafit (3) are examples of utilities based on rules and a greater or lesser degree of dependence on instrument performance.

I had an instructive conversation with Kirsten Hobby, one of the architects of the algorithm work in Mass Lynx software (Waters) a few years ago who has since started his own consulting software design company. He said, "We must make sure we clearly define the difference between (such algorithms as) i-FIT and Element Prediction Filters. Tools such as i-FIT do not reduce the number of elemental compositions but complement them and are independent of prediction algorithms."

The "fitting" algorithm is an accurate mass and isotope ratio correlation tool. Photodiode-array (PDA) detectors have offered a utility that measures a nominal data sample (typically the most abundant in a "peak") against other data samples in the same peak for similarity. An algorithm such as i-FIT similarly makes a comparison between the experimental data and each of the proposed candidates within a defined mass/ppm tolerance. The comparison is made between both the accurate mass and the intensity of the M, M+1, and M+2 peaks. The mass and intensity comparisons are weighted (independently), to afford some compensation for experimental variations in peak intensity and mass accuracy. The outcome is the value created for each of the proposed candidate formulae. A perfect fit would theoretically give a value of zero, although obviously that is not likely to happen experimentally. The general approach is to rank the list according to value: the result appearing at the top is the formula with an isotope cluster that best matches the experimental data.

According to Hobby's view, "There are two important points to make here. First, the formula with the lowest value is simply the best fit, not necessarily the correct formula. Second, and more importantly, the actual value has no significance on its own. Therefore it is not possible to include/exclude individual formulae on the basis of i-FIT values. The i-FIT values in the list have significance for each candidate relative to the experimental data in terms of 'goodness of fit.'

Whether the correct formula is the best 'fit' depends on a number of parameters including the performance of the instrument, the choice of elements in the elemental composition analysis, and the mass/ppm tolerance applied during the elemental composition analysis.

There are instances where quantitative results might be had assuming a level of accuracy in isotope ratio measurement. An experimental error of <3% in isotope ratio measurement might be sufficient to identify a compound uniquely, but likely only true in a limited environment such as target analysis against a database (4)."

Hobby makes a case (5) where assumptions could not be made about limited experimental error and still yield useful results: "For some compounds with errors in the M:M+2 ratio in the order of 20%," he says, "it was possible to get unequivocal formula identification with Element Prediction Filters."

Element prediction filters: As described by Hobby, the element prediction filters are a spectral interpretation tool that "estimates elemental composition using 'chemistry' " (that is, natural isotope abundances) and not instrument performance. Currently, you can use compounds with C, H, N, O, P, F, Na, Cl, Br, and S. The element prediction filters are not strictly an accurate mass tool. They work with nominal mass data, although their application best suits accurate mass data.

In addition, two notable improvements in our understanding over the textbook interpretations for sulfur and carbon have come to light recently. In the case of sulfur, you can accurately estimate the number of S at high mass (for example, 1000 Da) and also simultaneously estimate S in the presence of chlorine or bromine. In the case of carbon, more accurate estimates can be made compared to the historical method of dividing the M:M+1 ratio by the natural abundance of ¹²C (1.07%).

If you are going to use instrument performance to restrict the candidate elemental composition, as suggested by Kind and Fiehn (6), you may need preexisting evidence for errors in isotope ratio measurement from the instrument you are going to use. Hobby's experience at the time shows the error in isotope ratio measurement is variable, not simple to define, and it correlates more with elemental composition than with mass. An example taken from Hobby's ASMS talk in 2006, illustrates how he could "eliminate 99.73% of the "incorrect," which agrees with the >95% that Kind and Fiehn quote for an instrument operating at 3 ppm and with a 2% isotope ratio error."

The first question any practitioner asks is: Can I use the mass spectral data to decide what is the elemental composition and probable structure of my unknown species?

According to Hobby the answer is "Yes" providing you understand how "good" (or "bad") the data are. If the mass spectral data were perfect then there would be no problem, but alas we are far from perfection and so you must accept that the mass spectral data will always have errors in both mass and isotope ratio accuracy. The key to the solution is quantifying the imperfection, and this can only be done by a statistical analysis of the accuracy and precision of the mass spectral data.

The majority of the solutions in the field use what Hobby calls "quantitative mass spectral scoring" (for example, Waters' i-FIT, Bruker's Sigma-FIT, and Cerno Bioscience's Spectral Accuracy). In other words, these methods assume the experimental data will correlate with the theoretical data very well and take no account of the inherent experimental errors in the raw data. As we have seen there are examples in the literature that show that there is certainly no guarantee that the correct formula will be the "best fit."

In Hobby's estimation, "To use instrument performance to restrict the candidate formula list would have been far simpler. But in practice it may be more difficult to apply successfully."

Advances in isotope utility: Hobby has in recent years carried his design on as Kisotopic Solutions in the UK (7). His recommendation is "Do not ask 'which formula is correct?' but 'how many formulae are statistically probable candidates?'"

"In practice you must sample the experimental errors in situ (at least once) and then incorporate the probable distribution of errors in mass and isotope ratio accuracy into the analysis of an unknown. Hence you are taking a pragmatic approach. The result dataset could be a single probable formula, but alternately there could be multiple possibilities that would have to be considered equally likely because the instrument does not have sufficient mass or isotope ratio accuracy to discriminate between those formulae. The number of statically probable candidates is also affected by both the mass and actual elemental composition of the unknown molecule, in addition to the inaccuracies in the raw mass spectral data.

Hobby's approach, dubbed "Spectral Simplicity," is to automatically apply the statistical analysis and then simplify the result dataset to eliminate the need for any interpretation by the user. Thus the answer is a "yes" or "no," not a number whose "quantitative significance" is open to interpretation. The process was named "FuzzyFit" indicating there is some fluidity in the correlation of the experimental mass spectra with theoretical.

As in most software approaches Spectral Simplicity has three layers of processing and each step literately reduces the number of probable candidate formulae. The steps are

• Generate candidate molecular formulas using the MS data and select the statistically probable candidates.

• Generate candidate molecular formulas for the fragment ion and neutral loss species and eliminate formulas that do not correlate with proposed molecular formulas.

• Apply any fragmentation relationship information (that is, fragment "3" comes from fragment "2," and so forth) to the fragment ion species and eliminate formulas that do not correlate with proposed molecular formulas.

Richard Denny, principal software engineer (Waters Manchester, UK) with current interests in prediction algorithm design commented "Instrument performance in terms of mass accuracy and the assumption of Poisson (counting) statistics for the intensities is at the heart of the calculation of values as found in tools such as I-Fit. In fact, the development from earlier versions to the more quantitative version we have today is due to reporting the posterior probability (or Fit Confidence %) correctness of a composition.

It is always important to note that this probability is conditional on assumptions made in constructing the space of compositions to search, instrument performance (mass accuracy and the applicability of Poisson statistics) as well as, of course, the observed data. While it may be difficult to distinguish the correct composition among others allowed by the search the Fit Confidence % (posterior probability) shows that, given the assumptions and the data, one compound is probably correct among all the other compositions considered sharing similar posterior probability.

Now users have a clear and quantitative way of discriminating against unlikely compositions. However, probabilities are always conditional on assumptions, so care must be taken in setting the search parameters for the algorithm." Today regardless of the approach and type of data used prediction tools equipped with fitting capabilities produce probabilities for the candidate compositions.

Michael P. Balogh is principal scientist, MS technology development, at Waters Corp. (Milford, Massachusetts); a former adjunct professor and visiting scientist at Roger Williams University (Bristol, Rhode Island); cofounder and current president of the Society for Small Molecule Science (CoSMoS); and a member of LCGC's editorial advisory board.

This article first appeared as an installment of Michael Balogh's "MS—The Practical Art" column in the February 2010 issue of LCGC North America.

References

(1) Icons of Chromatography: Harold McNair, www.chromatographyonline.com Nov 1 2009.

(2) A.H. Grange, J.R Donnelly, G.W Sovocool, and W.C. Brumley, Anal. Chem. 68, 553–560 (1996).

(3) M. Pelzing, C. Neusub, and M. Macht, LCGC Eur. 17(11a), 38–39 (2004).

(4) S. Ojanpera, A. Pelander, M. Pelzing, I. Krebs, E. Vuori, and I. Ojanpera, Rapid Commun. Mass Spectrom. 20(7), 1161–1167 (2006).

(5) K. Hobby and R. Bateman, "The Use of Isotope Ratio Measurements to Reduce the Number of Candidate Elemental Compositions from Accurate Mass Determination," Proceedings of the 54th ASMS Conference on Mass Spectrometry and Allied Topics, Seattle, Washington, May 28– June 1, 2006

(6) T. Kind and O. Fiehn, LCGC 26(2), 176–187 (2008).

(7) K. Hobby, R.T. Gallagher, P. Caldwell, and I.D. Wilson, Rapid Commun. Mass Spectrom. 23(2), 219–227.

(8) J.R. de Laeter, J.K. Böhlke, P. De Bièvre, H. Hidaka, H.S. Peiser, K.J.R. Rosman, and P.D.P. Taylor, Pure Appl. Chem. 75(6), 683–800 (2003).