Neutron Spectroscopy
Not all spectroscopy uses light . . .

Most of us are at least nominally aware that light (rather, electromagnetic radiation) is not the only possible probe of matter and its behavior. One type of analysis uses neutrons as the probe of matter. As such, this is a form of neutron spectroscopy, or as it is more commonly called, neutron scattering. Neutron scattering is separated into two types: elastic neutron scattering and inelastic neutron scattering. In elastic neutron scattering, the neutrons have the same energy coming out of a sample as they did going in, while in inelastic neutron scattering the energy of the neutrons changes because of their interaction with matter. Here I will briefly introduce both types of scattering.

David W. Ball
Sources of Neutrons
Neutrons are a kind of subatomic particle normally found in the nucleus of atoms. Hence, production of neutrons invariably requires nuclear processes. A common source of neutrons for research (as opposed to power generation) purposes is a small nuclear reactor that uses low-enriched uranium, or LEU. LEU is defined as uranium enriched in 235 U at concentrations less than 20% (natural uranium consists of 0.7% 235 U). According to the International Atomic Energy Agency's web site (1), at this writing there are currently 235 reactors around the world that are supplying neutrons for research purposes.
The other way of generating neutrons is by spallation, which is the name given to the process by which a target is hit with a projectile and pieces of the target are ejected as a result. In nuclear spallation, hydride ions (H– ) are accelerated by a particle accelerator, then stripped of their electrons down to the bare proton, which is accelerated further and directed to a heavy metal (like tantalum or mercury) target. As many as 20–30 neutrons are given off by the metal nucleus for each proton that impacts the nuclei. The neutrons are then directed toward various experiments. The person who first envisioned nuclear spallation? Glenn Seaborg.
In many circumstances, neutrons that are produced by either method are too high in energy, so their energies must be decreased before they are used; we say that the neutrons must be moderated. Materials that moderate neutrons include light and heavy water, beryllium, and graphite.
Neutrons are classified by their energies (expressed in electron-volts, eV), which are directly related to their velocities (in meters or kilometers per second) and temperatures (in kelvins). For a particle the size of a neutron (1.675 × 10–27 kg), 1 eV of energy corresponds to a velocity of 13.8 km/s; keep in mind that the energy of a neutron depends on the square of the velocity (remember, K = ½ mv2 ). As such, classification can imply a neutron's velocity or its temperature. Fast neutrons have an energy of 0.1–1 MeV (megaelectron-volt), or a velocity of 4000–14,000 km/s. Slow neutrons have an energy of 100 eV or less, corresponding to a velocity of 138 km/s. (Take these numbers with a grain of salt; references can differ greatly about the energy and velocity cutoffs. It should be clear, however, that fast neutrons are, well, faster and more energetic than slow neutrons.)
Thermal neutrons have an average temperature of room temperature, or about 295 K. This corresponds to an energy of 0.025 eV and a velocity of 2.2 km/s. Neutrons with an energy/velocity/temperature higher than this are called hot neutrons, and neutrons with an energy/velocity/temperature lower than this are called cold neutrons. Even within cold neutrons, there are other classifications, going down to ultracold neutrons, which have energies in the range of nanoelectron-volts and velocities on the order of meters per second.
One other thing to remember is that neutrons have an equivalent wavelength given by the de Broglie relation:
λ = h/p = h/mv
where λ is the de Broglie wavelength in meters, h is Planck's constant in units of joule-seconds, m is the mass of a particle in kilograms, and v is the velocity of the particle in meters per second. For a neutron, h and m are constants (we're assuming that most velocities are nonrelativistic, or that relativistic corrections — which for these neutrons are on the order of 1.5% at most — can be ignored), so the de Broglie relation reduces to
λ = (3.956 × 10–7)/v
Thus, neutron wavelengths range from 2.8 × 10–14 m (0.00028 Å) or smaller for fast neutrons to 1.8 × 10–10 m (1.8 Å) for thermal neutrons to 4.95 × 10–8 m (495 Å, which is the same wavelength as extreme ultraviolet [EUV] light) for ultracold neutrons. Some forms of neutron scattering take advantage of the wave nature of neutrons.
Elastic Neutron Scattering
One application of elastic neutron scattering is neutron diffraction to determine structures of solid, liquids, and gases. Taking advantage of the neutron's wave properties, neutron diffraction is very similar to X-ray diffraction. For example, it obeys the Bragg equation:
nλ 2d sin Θ
where λ is the de Broglie wavelength of the neutrons, d is the distance between adjacent planes of scattering particles, Θ is the angle between the incoming neutron source and the plane of the scattering particles, and n is an integer called the order of the diffraction. Diffraction of neutrons is based on the production of constructive interference of the waves, as shown in Figure 1.
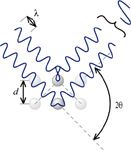
Figure 1: Illustration of the geometry of the Bragg equation.
Neutron diffraction has some advantages over X-ray diffraction. Perhaps most importantly, neutrons are diffracted from atomic nuclei rather than from electron clouds, so exact atomic positions are more accurately determined and hydrogen shows up explicitly (hydrogen atoms do not diffract X-rays well). Neutrons diffract better at high angles as well as low angles, so larger scattering angles can be probed, again increasing the resolution of the experiment. Because of the higher accuracy, neutron diffraction can be used to study the stress behavior of solids.
Neutron diffraction suffers by requiring larger sample sizes, so single crystal neutron diffraction is rare; powdered samples are the norm. Certain atomic nuclei are also strong absorbers of neutrons, so they are not strong scatterers. The scattering vs. absorption of neutrons is isotope-dependent, so different isotopes of the same element can be noticed.
Elastic neutron scattering can also be used for reflectometry, which is a technique used to study thin films. As with neutron diffraction, neutron reflectometry provides complementary information compared to X-ray reflectometry.
Inelastic Neutron Scattering
In inelastic neutron scattering, the neutrons interact with a sample in such a way as to change their energies, getting either more or less energetic. In this regard, inelastic neutron scattering is very similar to classic forms of spectroscopy. Indeed, the experimental setup is also similar, as shown in Figure 2. Some forms of inelastic neutron scattering use a monochromator, while others do not.
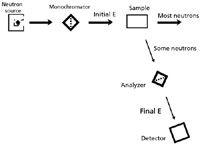
Figure 2: Schematic of an inelastic neutron scattering experiment. Note its similarity to a regular spectroscopic setup.
In time-of-flight scattering, a polychromatic neutron pulse is chopped or monochromated and then sent through a sample. The sample diffracts neutrons having certain wavelengths (that is, certain energies) and at certain angles. The angles are measured by position-sensitive detectors, but the wavelengths (and therefore energies) of the neutrons are determined by measuring how much time it takes for the neutron signals to reach a detector. This indicates the neutron's velocity, which is used in de Broglie's relation to get the wavelengths of neutrons that are diffracted. Then the Bragg equation can be used to determine structural information of the sample.
Neutron backscattering is a technique in which "diffraction" is set up so that the angles of the monochromator and analyzer are close to 90°. Fast neutrons are directed toward a sample and a portion of them are scattered back near the source. Because small nuclei are better at scattering fast neutrons, an increase in the backscattering indicates a relatively higher proportion of smaller atoms like hydrogen. Neutron backscattering is used to find water in arid regions and to look for explosives in unexploded land mines; it has obvious implications in airport security.
Neutron spin echo spectroscopy is an unusual form of spectroscopy that relies on the precession of a spinning neutron (spin quantum number = ½), although it is ultimately a type of time-of-flight measurement. A polarized beam of cold, polychromatic neutrons passes through a magnetic field, where the number of Larmor precessions of the neutrons are set depending on the length and strength of the magnetic field. The beam then scatters off a sample and the resulting precessions after scattering are determined using a second magnetic field. The difference in the number of precessions is an indication of the change in velocity — and therefore the change in energy — of the neutrons. In this case, however, the measurement is not a direct measure of the energy change, but is a time-dependent measurement that can be treated by a Fourier transform to convert it to the energy domain — that is, a spectrum. Neutron spin echo measurements have resolutions on the order of nanoelectron-volts.
Neutron triple-axis spectrometry allows for the variations of three dimensions by being able to rotate a sample (typically a single crystal), the monochromator, and the detector independently (2). Energies probed include phonon modes of solids. Amorphous systems, proteins, aggregate motions of polymers and biological molecules, and energy transfer processes in liquids and glasses can be studied. This technique has become so useful in the study of the condensed phases of matter that its developers were awarded the 1994 Nobel Prize in Physics:
The Nobel Prize in Physics 1994 was awarded "for pioneering contributions to the development of neutron scattering techniques for studies of condensed matter" jointly with one half to Bertram N. Brockhouse "for the development of neutron spectroscopy" and with one half to Clifford G. Shull "for the development of the neutron diffraction technique" (3).
This achievement was recently noted in Spectroscopy's timeline of events in the history of spectroscopy (4). Shull's Wikipedia entry (5) claims that this was the longest time between the individual work performed (1946) and the awarding of the prize to date.
David W. Ball is a professor of chemistry at Cleveland State University in Ohio. Many of his "Baseline" columns have been reprinted in book form by SPIE Press as The Basics of Spectroscopy, available through the SPIE Web Bookstore at www.spie.org. His book Field Guide to Spectroscopy was published in May 2006 and is available from SPIE Press. He can be reached at d.ball@csuohio.edu; his website is academic.csuohio.edu/ball
References
(1) International Atomic Energy Agency website, http://www.iaea.org. Accessed September 22, 2010.
(2) G. Shirane, S.M. Shapiro, and J.M. Tranquada, Neutron Scattering with a Triple-Axis Spectrometer: Basic Techniques (Cambridge University Press, 2002).
(3) http://nobelprize.org/nobel_prizes/physics/laureates/1994/. Accessed October 4, 2010.
(4) H. Mark and S. Brown, Spectroscopy 25(6), 34–41 (2010).
(5) http://en.wikipedia.org/wiki/Clifford_Shull. Accessed October 4, 2010.

New Study Reveals Insights into Phenol’s Behavior in Ice
April 16th 2025A new study published in Spectrochimica Acta Part A by Dominik Heger and colleagues at Masaryk University reveals that phenol's photophysical properties change significantly when frozen, potentially enabling its breakdown by sunlight in icy environments.