Connecting Chemometrics to Statistics - Part I: The Chemometrics Side

This series of columns has been running for a long time. Long-time readers will recall that it has even changed its name since its inception. The original name was "Statistics in Spectroscopy." This was a multiple pun, as it referred to the science of Statistics in the journal Spectroscopy and the science of Statistics in the science of Spectroscopy as well as statistics (the subject of the science of Statistics) in the journal Spectroscopy. [See our third column ever (1) for a discussion of the double meaning of the word "Statistics." The same discussion is found in the book based upon those first 38 columns (2).]

Our goal then, as now, was to bring the study of chemometrics and the study of statistics closer together. While there are isolated points of light, it seems that many people who study chemometrics have no interest in and do not appreciate the statistical background upon which many of our chemometric techniques are based, nor do they appreciate the usefulness of the techniques that we could learn from that discipline. Worse, there are some who actively denigrate and oppose the use of statistical concepts and techniques in the chemometric analysis of data. The first group can, perhaps claim unfamiliarity (ignorance?) with statistical concepts. It is difficult, however, to find excuses for the second group.

Nevertheless, at its very fundamental core, there is a very deep and close connection between the two disciplines. How could it be otherwise? Chemometric concepts and techniques are based upon principles that were formulated by mathematicians hundreds of years ago, even before the label "statistics" was applied to the subfield of mathematics that deals with the behavior and effect of random numbers on data. Nevertheless, recognition of statistics as a distinct subdiscipline of mathematics also goes back a long way, certainly long before the term "chemometrics" was coined to describe a subfield of that subfield.

Before we discuss the relationship between these two disciplines, it is, perhaps, useful to consider what they are. We have already defined "statistics" as ". . . the study of the properties of random numbers . . ." (3).

A definition of "chemometrics" is a little trickier of come by. The term originally was coined by Kowalski, but currently, many chemometricians use the definition by Massart (4). On the other hand, one compilation presents nine different definitions for "chemometrics" (5,6) (including "what chemometricians do," a definition that apparently was suggested only half humorously). But our goal here is not to get into the argument over the definition of the term, so for our current purposes, it is convenient to consider a somewhat simplified definition of "chemometrics" as meaning "multivariate methods of data analysis applied to data of chemical interest."

This definition is convenient because it allows us to then jump directly to what is arguably the simplest chemometric technique in use, and consider that as the prototype for all chemometric methods; that technique is multiple regression analysis. Written out in matrix notation, multiple regression analysis takes the form of a relatively simple matrix equation:

where B represents the vector of coefficients, A represents the matrix of independent variables, and C represents the vector of dependent variables.

One part of that equation, [A^T A]^-1 , appears so commonly in chemometric equations that it has been given a special name; it is called the pseudoinverse of the matrix A. The uninverted term: A^T A is itself fairly commonly found as well. The pseudoinverse appears as a common component of chemometric equations because it confers the least squares property on the results of the computations — that is, for whatever is being modeled, the computations defined by Equation 1 produce a set of coefficients that give the smallest possible sum of the squares of the errors, compared with any other possible linear model.

Huh? It does? How do we know that?

Well let's derive Equation 1 and see.

We start by assuming that the relationship between the independent variables and the dependent variable can be described by a linear relationship:

where β, as noted previously, represents the "true" or population values of the coefficients (1). Equation 2 expresses what is often called the "inverse least squares," or P-matrix, approach to calibration. Because we don't know what the true values of the coefficients are, we have to calculate some approximation to them. We therefore express the calculation in terms of "statistics," quantities that we can calculate from the data (see that same column for further discussion of these points):

How are we going to perform that calculation? Well to start with, we need something to base it on, and the consensus is that the calculation will be based on the errors, because in truth, Equation 3 is not exactly correct because C will in general not exactly equal bA. Therefore, we extend Equation 3:

Now that we have a correct equation, we want to solve this equation (or Equation 3, which is essentially equivalent) for b. Now, if matrix A had the same number of rows and columns (a square matrix), we could form its inverse, and multiply both sides of Equation 3 by A^-1 :

and because multiplying any matrix by its inverse results in a unit matrix, we find the following equations:

This is essentially the solution generated by solving simultaneous equations. This is fine if we can rely upon simultaneous equations for the solution to our data. In the general case, however, matrix A will not have the same numbers of rows and columns, and in fact, often it is necessary for matrix A to contain data from more samples than there are variables (that is, wavelengths, in spectroscopic applications). Therefore, we cannot simply compute the inverse of matrix A, because only square matrices can be inverted. Therefore, we proceed by multiplying Equation 3 by A^T :

The matrix formed by multiplying A by its transpose A^T is a square matrix, and, therefore, can be inverted. Therefore, if we multiply both sides of Equation 8 by the matrix inverse of A^T A, we have Equation 9:

And again, because any matrix multiplied by its inverse is a unit matrix, this provides us with the explicit solution for b, which was to be determined as follows:

Equation 10, of course, is the same as Equation 1, and therefore, we see that this procedure gives us the least-squares solution to the problem of determining the regression coefficients, and Equation 1 is, as we said, the matrix equation for the least-squares solution.

Huh? It does? It is? How do we know that?

Where, in this whole derivation, did the question of least squares even come up, much less show that Equation 10 represents the least-squares solution? All we did was a formalistic manipulation of a matrix equation to allow us to create some necessary intermediate matrices in a form that would permit further computations, specifically, a matrix inversion.

In fact, it is true that Equation 10 represents the least-squares solution to the problem of finding the coefficients of Equation 3, it is just not obvious from this derivation, based upon matrix mathematics. To demonstrate that Equation 10 is, in fact, a least-squares solution, we have to go back to the initial problem and apply the methods of calculus to the problem. This derivation has been done in great detail (7), and in somewhat lesser detail in a spectroscopic context (8).

Basically, what is done is that the linear relationship of Equation 3 is written out, for some (large) number of samples, and for some number of independent variables, although for reasons that will eventually become apparent, we leave out the constant (b₀) term. For our purposes, we limit the number of variables to two, although we assume that there are n samples (where n >> 2):

To summarize the procedure used from calculus (again, refer to either of the indicated references for the details), the errors are first calculated as the difference between the computed values (from Equations 11a and 11b) and the (unknown) "true" value for each individual sample; these errors are then squared and summed. This is all done in terms of algebraic expressions derived from equations 11. The "least square" nature of the desired solution is then defined as the smallest sum of squares of the error values, and is then clearly seen to be the minimum possible value of this sum of squares, that could potentially be obtained from any possible set of values for the set of computed values of b_i.

How is the "least square" set of coefficients computed? The methods of calculus give us the procedure to use, and it is the standard, first-term calculus procedure: take the derivative and set it equal to zero — this gives a minimum. In this case, it is (only slightly) more complicated in that we need to take the derivatives of the error expressions with respect to each b_i, because we want to compute the values for all the b_i that give the lowest sum-squared error.

The result of doing all this is expressed in a set of algebraic equations; for our two-variable case, these equations are (all sums are taken over the n samples):

Exercise for the reader: Derive Equations 12a and 12b from Equation 11, using the indicated procedure (recall that the summations are over all the samples).

Except for the various b_i, all the quantities in Equations 12a and 12b are measured data; therefore performing the indicated computations results in a set of numbers multiplying the various b_i and then the b_i can be calculated by solving Equations 12a and 12b as simultaneous equations.

Equations 12a and 12b, while derived from calculus, can be converted in matrix notation as follows (recall that in matrix multiplication, the rows of the left-hand operand are multiplied by the columns of the right-hand operand):

Factoring equation 13a:

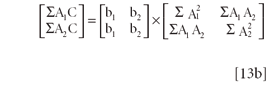
and then each matrix can be expanded into separate vectors, matrices, and matrix operations:

In compact matrix notation, Equation 14 is:

Equation 15 is the same as Equation 8. Thus, we have demonstrated that the equations generated from calculus, in which we explicitly inserted the "least square" condition, create the same matrix equations that result from the "formalistic" matrix manipulations of the purely matrix-based approach. Because the least-squares principal is introduced before Equation 8, this procedure therefore demonstrates that the rest of the derivation, leading to Equation 10, does in fact provide us with the least-squares solution to the original problem.

So now we have done a moderately thorough job of investigating the relationship between the calculus approach to least squares and the matrix algebra approach, based upon their chemometrics. But the original purpose of this column was stated to be an investigation of the relationship between chemometrics and statistics. What does our discussion here have to do with that? Come back and read the exciting conclusion in our next column.

Jerome Workman, Jr. serves on the Editorial Advisory Board of Spectroscopy and is director of research, technology, and applications development for the Molecular Spectroscopy & Microanalysis division of Thermo Electron Corp. He can be reached by e-mail at: jerry.workman@thermo.com

Howard Mark serves on the Editorial Advisory Board of Spectroscopy and runs a consulting service, Mark Electronics (Suffern, NY). He can be reached via e-mail: hlmark@prodigy.net

References

(1) H. Mark and J. Workman, Spectroscopy 2(3), 47–49 (1987).

(2) H. Mark and J. Workman, Statistics in Spectroscopy , 1st ed. ( Academic Press, New York, 1991).

(3) H. Mark and J. Workman, Spectroscopy 2(1), 38–39 (1987).

(4) D.L. Massart, B.G.M. Vandeginste, S.N. Deming, Y. Michotte, and L. Kaufman, Chemometrics: A Textbook (Elsevier Science Publishers, Amsterdam, 1988).

(5) J. Workman, Newslett. N. Am. Ch. Int. Chemomet. Soc., p. 3–7 (2002).

(6) J. Workman, Chemomet. Intell. Lab. Syst. 60, 13–23 (2002).

(7) N. Draper and H. Smith Applied Regression Analysis, 3rd ed. (John Wiley & Sons, New York, 1998).

(8) H. Mark, Principles and Practice of Spectroscopic Calibration (John Wiley & Sons, New York, 1991).