Headspace Raman Spectroscopy

We examine vapor-phase Raman spectroscopy through the acquisition of spectra from gas molecules confined to the headspace of sealed containers. Studying the Raman spectra of the liquid and vapor phases of compounds with different functional groups, degrees of hydrogen bonding, and polarity provides insight into the energetics of molecular interactions.

You were probably first introduced to rotational and vibrational-rotational spectroscopy as an undergraduate. Perhaps you even applied what you were learning in the lecture hall and from text books in a physical chemistry laboratory involving infrared absorption spectroscopy of gases. If so, that may well have been your last encounter with vibrational spectroscopy of compounds in the vapor phase.

Those of us who perform Raman spectroscopy do so almost entirely with materials in the condensed phase; that is, liquids or solids. However, many of the compounds with which we work have some measure of volatility, particularly liquids that evaporate quite rapidly, such as methanol, isopropyl alcohol, and acetone. Consequently, sealed containers of compounds, solutions, or mixtures will have some number of volatilized molecules in the headspace between the condensed phase and the container seal. A transparent container offers Raman spectroscopists the ability to probe both the condensed and vapor phase in the headspace above the sample.

In this installment, we examine vapor-phase Raman spectroscopy through the acquisition of spectra from gas molecules confined to the headspace. Comparisons of the vapor-phase and condensed-phase spectra reveal the significant effects of molecular interactions, particularly hydrogen bonding, on the vibrational spectrum. The degree to which certain Raman bands differ in energy and bandwidth (primarily from collisional broadening) between the vapor and condensed phases provides insight into the variation of molecular interactions of compounds of different molecular structure and functional groups. We also explore the phenomenon of Fermi resonance and discuss the effect of spin statistics on high spectral resolution vibrational-rotational diatomic molecules.

Carbonated Beverages

Carbonated beverages such as soda, beer, or sparkling water have a substantial amount of CO₂ dissolved in them, which provides the fizz when first opening the bottle or can and the tingle when drinking the contents. We've all experienced drinking a soft drink that has lost most of its CO₂; we say the drink has gone flat. Our own experience with beverages that have gone flat teaches us that CO₂ is not particularly soluble in water at atmospheric pressure and, for that reason, carbonated beverages must be securely sealed. Consequently, carbonated beverages have a high partial pressure of CO₂ in the headspace.

One such carbonated beverage is beer. Fluorescence overwhelms the Raman scattering from the liquid portion of the sealed beer sample when using 532-nm excitation (the excitation wavelength for all spectra shown in this article). However, guiding the laser beam above the liquid through the headspace yields the spectrum of CO₂ shown in Figure 1. One of the most striking features of Raman spectra from the vapor phase are how narrow the bands are relative to those obtained in the liquid phase. The full width at half maximum (FWHM) of the CO₂ bands is 0.9 cm^-1 ! The spectrum consists of six bands: one attributed to O₂ and the remaining five bands attributed to CO₂. This may seem a little strange given that group theory predicts only one Raman active mode for CO₂, the ν₁ symmetric stretching mode.

Figure 1: Raman spectrum of CO2 and O2 from the headspace of beer.

A phenomenon called Fermi resonance accounts for the appearance of multiple CO₂ Raman bands. The symmetric stretching mode of CO₂ is of Σ⁺_g symmetry and is expected at approximately 1330 cm^-1 (1). The ν₂ doubly degenerate bending mode is Raman forbidden, but does appear in the infrared absorption spectrum at 667 cm^-1 (2). However, the overtone (2ν₂) has Σ⁺_g symmetry and is expected at 1334 cm^-1. So, we have a fundamental vibrational mode and an overtone of approximately equal energies and the same symmetry. Therefore, these two energy states can interact, and this interaction is called Fermi resonance. This type of resonance can produce quite striking effects with respect to both Raman scattering strength and perturbation of the vibrational states — that is, Raman band positions.

The assignments of the beer headspace CO₂ Raman bands are shown in Table I in accordance with the assignments of Hanf and coworkers (3). The very strong bands at 1284.8 and 1387.5 have been assigned to ν₁ and 2ν₂, respectively. Fermi resonance has caused the ν₁ and 2ν₂ bands of approximately equal energy to split such that the lower energy state shifts lower and the higher energy state shifts higher. The greater the interaction of the two states (that is, the stronger the Fermi resonance), the greater the splitting of the energy states and the observed Raman bands. Here, we see a difference of 103 cm^-1. In addition to the band splitting, one also observes a so-called borrowing of intensity with Fermi resonance. Normally, one would expect the 2ν₂ Raman band to be comparatively weak. However, the 2ν₂ band at 1387.5 cm^-1 is more intense than the ν₁ fundamental band at 1284.8 cm^-1. Also, the strength of the Fermi resonance is so great that isotopic (¹³ C¹⁶ O₂) and excited state or so-called hot (ν₁¹ and 2ν₂¹) bands appear in the Raman spectrum.

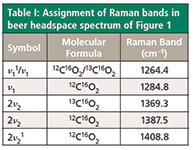
Table I: Assignment of Raman bands in beer headspace spectrum of Figure 1

The Raman spectra obtained from sparkling water offer us an opportunity to compare the spectrum of CO₂ in the vapor phase with that dissolved in water. Raman spectra of CO₂ and O₂ from the headspace of sparkling water and the liquid itself are shown in Figure 2. The headspace Raman spectrum of sparkling water is nearly identical to that from beer. Now, without the overwhelming fluorescence generated by the liquid beer, the Raman spectrum of the CO₂ in liquid sparkling water can be obtained. The liquid spectrum consists of bands at 1272.7 and 1379.6 cm^-1 (CO₂) and 1633.6 cm^-1 (the bending mode of H₂O). The effect of the solvent (H₂O) on the solute (CO₂) can be seen in the positions and widths of the CO₂ ν₁ and 2ν₂ bands. The shifts between the vapor phase and the water solubilized CO₂ ν₁ and 2ν₂ bands are -12.3 and -8.1 cm^-1, respectively. Given that the shift in the ν₁ band is 50% greater than that observed for the 2ν₂ band, it is not surprising that the intensity of the solubilized CO₂ ν₁ band is significantly more diminished. Also, the FWHM of the 2ν₂ bands in the vapor phase and water solubilized CO₂ are 0.9 and 9.9 cm^-1, respectively. The band width of the solvated CO₂ is 10 times greater than that in the vapor phase, thereby indicating the strength of the interactions of CO₂ with the water solvent. The Raman spectra of the headspace and solvated CO₂ demonstrate that Raman spectroscopy is well suited for the study of molecular interactions of solute and solvent.

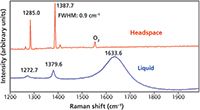
Figure 2: Raman spectra of CO2 and O2 from the headspace of sparkling water and the liquid.

Effect of Hydrogen Bonding on the Vibrational Spectrum

In the previous section, we compared the spectra of a gas in the vapor phase and solubilized by water. Here, we compare the spectra of compounds in the liquid and vapor phases and see the effect of hydrogen bonding manifest in the vibrational spectrum of the liquid. Our first example consists of household ammonia purchased at the grocery store. In this case, our headspace Raman spectrum consists of both the solute (NH₃) and solvent (H₂O). The Raman spectra of the liquid and headspace of household ammonia are shown in Figure 3. The spectrum of the liquid consists of a very broad band ranging from approximately 3000 cm^-1 to 3700 cm^-1 and consisting of two partially resolved broad peaks. This is the Raman scattering due to water and the enormous bandwidth is attributed to hydrogen bonding. The much narrower peak protruding at 3314 cm^-1 is the ν₁ symmetric stretch of NH₃. The Raman bandwidths clearly indicate that the strength of hydrogen bonding among water molecules is far greater than that with ammonia molecules.

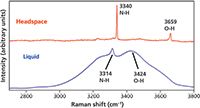
Figure 3: Raman spectra of liquid- and vapor-phase household ammonia.

In fact, the effects of hydrogen bonding are made stunningly clear when one compares the liquid spectrum to that of the headspace. The NH₃ symmetric stretch in the vapor phase is much narrower and is shifted relative to the solvated species by 26 cm^-1. The absence of solvation by the water molecules reduces the molecular interactions and collisional broadening and thereby causes the NH₃ symmetric stretching mode to shift to higher energy and narrows the distribution of vibrational states. Hydrogen bonding is even more significant in the liquid phase of water, so the difference between OH stretching bands from water in the liquid and vapor phases is even more dramatic. Without the contribution from hydrogen bonding, the OH stretching bands narrow significantly and shift to 3659 cm^-1 where a single asymmetric band appears.

Hydrogen bonding plays an important role in the molecular interactions of the polar solvent methanol. Raman spectra of methanol in the liquid and vapor phase are shown in Figure 4. Raman scattering from the CH stretching vibrational modes appear at energies less than 3000 cm^-1. The OH stretch of methanol appears as a broad band centered at 3340 cm^-1 in the liquid phase; however, it splits into two partially resolved bands at 3684 and 3697 cm^-1 in the vapor phase. That is a shift of approximately 350 cm^-1, which can be attributed to hydrogen bonding. The CH stretching modes are also affected, but to a substantially lesser degree. The 2832 and 2941 cm^-1 bands shift to 2846 and 2956 cm^-1, a shift of 14 and 15 cm^-1, respectively.

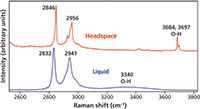
Figure 4: Raman spectra of liquid- and vapor-phase methanol.

These differences in Raman band positions between the liquid and vapor phases provide insight into the energetics of the molecular interactions in the liquid phase. Of course, hydrogen bonding offers the strongest type of molecular interaction that we can expect to see, and compounds bearing OH functional groups can be expected to exhibit hydrogen bonding and have strong molecular interactions. However, as the nonpolar portion of the molecule becomes larger or the polar functional group is removed, we can expect the energetics of molecular interaction to diminish. Compounds of medium polarity or entirely nonpolar can be expected to have smaller differences between the Raman spectra of the liquid and vapor phases.

Organic Compounds with Different Strengths of Molecular Interactions

Acetonitrile is considered a medium polarity solvent that is miscible with many organic solvents (except saturated hydrocarbons) and water. For the purposes of our discussion, we can think of it as having replaced the OH group on methanol with the CN nitrile group. Therefore, we might expect that the differences between the liquid- and vapor-phase CH₃ stretches of acetonitrile might be comparable to those of methanol. However, that expectation is not met in the Raman spectra of the liquid and vapor phase of acetonitrile shown in Figure 5.

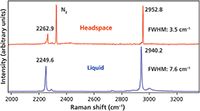
Figure 5: Raman spectra of liquid- and vapor-phase acetonitrile.

The Raman spectrum of the liquid phase features two strong bands at 2249.6 and 2940.2 cm^-1 attributed to the CN stretch and CH₃ stretch, respectively. Note that the CH₃ stretch bandwidths of both liquid- and vapor-phase acetonitrile are significantly narrower than those observed in either liquid- or vapor-phase methanol spectra. In fact, the acetonitrile CH₃ stretch has a FWHM of only 7.6 cm^-1 in the liquid phase and is reduced by approximately 50% to 3.5 cm^-1 in the vapor phase. As expected, the CN stretch and CH₃ stretch bands shift to higher energy in the vapor phase, 2262.9 and 2952.8 cm^-1. It is noteworthy that the phase-related energy shifts are 13.3 and 12.6 cm^-1 for the CN and CH stretches, respectively. Those shifts are approximately equal and slightly less than the 14–15 cm^-1 difference that we observed for the CH stretching in methanol. Comparing all of these spectral features and their differences in the acetonitrile and methanol spectra, we can infer that the molecular interactions of methanol are greater than those of acetonitrile.

Our comparison of the Raman spectra of liquid and vapor phases now progresses to the nonpolar solvent benzene. We expected the molecular interactions to be weak compared to those of polar and medium polarity solvents. The Raman spectra of benzene in the liquid and vapor phase shown in Figure 6 confirm that expectation. Here, we focus our attention on the ring breathing mode, which appears at 991.4 cm^-1 with a FWHM of 2.1 cm^-1 in the liquid spectrum. The Raman band assigned to the ring breathing mode of benzene in the liquid phase is actually narrower than any of the bands from either methanol or acetonitrile in the vapor phase. This is a measure of just how weak the molecular interactions are. Nevertheless, the vapor-phase spectrum reveals a shift of the ring breathing mode band of +0.7 cm^-1 to 992.1 cm^-1 and a narrowing of the FWHM to 1.1 cm^-1. So that even when the molecular interactions in the liquid phase are weak, it is clear that in the vapor phase they are still weaker.

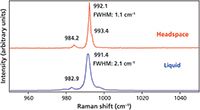
Figure 6: Raman spectra of liquid- and vapor-phase benzene.

Studying the Raman spectra of the liquid and vapor phases of compounds with different functional groups, degrees of hydrogen bonding, and polarity provides insight into the energetics of molecular interactions.

Vibrational-Rotational Raman Spectra of Atmospheric Molecules

We now move from compounds that are liquid at room temperature to atmospheric diatomic molecules. The primary components of air are N₂ and O₂. Therefore, we can expect to find a contribution from these molecules in most headspace Raman spectra. Having no dipole moment, these molecules are of course infrared inactive. However, because the polarizabilities of these molecules are anisotropic, one can observe Raman active rotational transitions in both the rotational and vibrational-rotational spectra. A discussion of the fundamental molecular physics and nuclear spin statistics of rotational and vibrational-rotational Raman spectroscopy is beyond the scope of this installment. Nevertheless, you will need to know just a few facts about the quantum mechanics of vibrational-rotational Raman spectroscopy to appreciate what you observe in the spectra of N₂ and O₂.

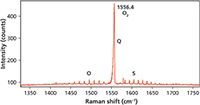
Figure 7: Raman spectrum of oxygen in air. Note the rotational side bands to the symmetric stretch at 1556.4 cm-1.

The selection rules for the vibrational-rotational Raman spectrum of a diatomic molecule are given by

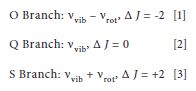
where J is the rotational quantum number. Note that the Raman selection rules differ from the rotational infrared active absorption selection rule of Δ J = ±1. An additional consideration is that the rotational wavefunction must have parity such that the overall wavefunction is symmetric. A consequence of these rules is that for O₂ with a total spin of 0, the rotational lines originating from a J state with an even number will be missing. In contrast, N₂ has a total spin of 1 and the rotational lines originating from all J states will be Raman active. We simply state here without detailed explanation that nuclear spin statistics dictate that for N₂, which has a total spin of 1, the intensity ratio of alternate lines is 2:1, whereas O₂ with a total spin of 0 has an intensity ratio of 1:0.

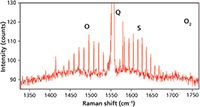
Figure 8: Raman spectrum of oxygen in air featuring the rotational side bands. The FWHM of the rotational side bands are 1.01 cm-1.

Now we are prepared to understand the vibrational-rotational Raman spectra of these atmospheric diatomic gases that are likely to be observed in any Raman headspace measurement. The vibrational-rotational Raman spectrum of O₂ in air is shown in Figure 7. The spectrum consists of the main vibrational symmetric stretch or Q branch at 1556.4 cm^-1. The O and S rotational branches can be seen on the low and high energy sides of the Q branch, respectively. Changing the intensity scale of Figure 7, we now have an expanded view of the rotational side bands as seen in Figure 8. The narrow peaks on either side of the Q branch correspond to the vibrational-rotational Raman selection transitions described in the equations above. The side bands of O₂ are all separated by two J states, originate from odd valued J states, and the intensities are all evenly distributed proportional to the populations of the original states. Note how narrow the O₂ sidebands are with a FWHM of 1.01 cm^-1.

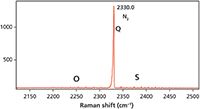
Figure 9: Raman spectrum of nitrogen in air. Note the rotational side bands to the symmetric stretch at 2330.0 cm-1.

The vibrational-rotational Raman spectrum of N₂ in air is shown in Figure 9. The Q branch of N₂ is significantly stronger than that of O₂, primarily because its concentration in the atmosphere is significantly higher than that of O₂. Note also that the O and S rotational sidebands are significantly weaker than those of O₂. Nevertheless, expansion of the intensity scale as seen in Figure 10 reveals the alternating 2:1 intensity of the sidebands as predicted by nuclear spin statistics. The side bands are all separated by one J state, originate from even and odd valued J states, and the intensities are all evenly distributed proportional to the populations of the original states and with respect to nuclear spin statistics. The O and S rotational sidebands of N₂ with a FWHM of 0.77 cm^-1 are even narrower than those of O₂.

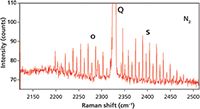
Figure 10: Raman spectrum of nitrogen in air featuring the rotational side bands. The FWHM of the rotational side bands are 0.77 cm-1.

Conclusions

We presented vapor-phase Raman spectra of dissolved gases that exhibit Fermi resonance. The liquid- and vapor-phase Raman spectra of nonpolar, medium polarity, and polar solvents were analyzed and the differences demonstrated that Raman spectroscopy is well suited for studying the energetics of molecular interactions. Finally, vibrational-rotational Raman spectroscopy was demonstrated with the atmospheric components of N₂ and O₂.

References

(1) C.N. Banwell, Fundamentals of Molecular Spectroscopy, 3rd ed. (McGraw-Hill, London, 1983), p. 96.

(2) L.A. Woodward, Introduction to the Theory of Molecular Vibrations and Vibrational Spectroscopy (Oxford, London, 1972), p. 348.

(3) S. Hanf, R. Keiner, D. Yan, J. Popp, and T. Frosch, Anal. Chem. 86, 5278–5285 (2014).

David Tuschel David Tuschel is a Raman applications manager at Horiba Scientific, in Edison, New Jersey, where he works with Fran Adar. David is sharing authorship of this column with Fran. He can be reached at: david.tuschel@horiba.com