Peak Shape and Closely Spaced Peak Convolution in Raman Spectra
Peak-fitting software is frequently written to offer the user a choice of automated peak fitting or one that allows the user to enter specific values of peak shape, amplitude, and width. The shapes are most often presented as a choice of percent Gaussian or Lorentzian profile contributions to the peak. To better understand these spectral profiles, we briefly explain the physical basis of the so-called spectral line shapes. Furthermore, we discuss and model the spectral shape, bandwidth, and broadening to help the reader see how the percentage of Gaussian and Lorentzian components contribute to overall peak shape and how two closely spaced and unresolved peaks of different amplitudes or bandwidths can affect the maximum position and overall appearance of the convolved peak.
Those who perform Raman spectroscopy know that acquiring a Raman spectrum is only the first step. What follows is often a detailed analysis of the individual peaks that make up the spectrum. The analysis step is usually performed using the spectral analysis and processing software provided by the vendor of the Raman instrument or a more general scientific data analysis software package. In the former case, one usually finds analysis tools for peak fitting. The peak fitting software is frequently written to offer the user a choice of so-called automated peak fitting or one that allows the user to enter specific values of peak shape, amplitude, and width. The shapes are most often presented as a choice of percent Gaussian or Lorentzian profile contributions to the peak.
The automated fitting routines can sometimes seem like a “black box” to those unfamiliar with spectral line width theory, peak shape, and the mechanisms for spectral line broadening. When the autofit routine generates an excessive number of peaks or some that seem unusually broad, it is understandable if the user doubts the chemical or physical basis for the fitted peaks and their contributions. After all, the program tries to generate a set of peaks that when added together leaves the least amount of residual between the sum of the peaks and the acquired spectrum. The best mathematical fit doesn’t always make good chemical or physical sense, which is why it is important for the user of these peak fitting tools to have some basic understanding of spectral line width theory and how two closely spaced and unresolved peaks can contribute to the shape and appearance of the single convolved peak that they produce. One can frequently find explanations of varying detail on spectral line width and broadening in books dedicated to spectroscopy. More specifically, there are several publications that can assist the interested reader with excellent explanations on spectral line shape as it relates to Raman spectroscopy (1–3).
The purpose of this installment of “Molecular Spectroscopy Workbench” is to contribute to the body of work on spectral line width and broadening by helping the reader see how the percentage of Gaussian and Lorentzian components contribute to overall peak shape, and how two closely spaced and unresolved peaks of different amplitudes or bandwidths can affect the maximum position and overall appearance of the convolved peak.
Gaussian and Lorentzian Contributions to a Single Peak
It is important how a qualitative understanding of how the Gaussian and Lorentzian profiles contribute to a single peak shape. Although a thorough explanation of the underlying chemical physics contributing to peak shape is beyond the scope of this work, you can find detailed explanations of the underlying bases for Gaussian and Lorentzian line shapes in the literature (1–3). Here, we give a brief description of the theory of these two profiles, show how they differ graphically, and reveal how the percent contribution of Gaussian and Lorentzian profiles affects the appearance of a single peak.
The spectral profiles are primarily determined by two lifetimes involving the excited state. Raman relaxation from the excited virtual state to the final vibrational state occurs within several picoseconds (10–12 s). The lifetime involved in this relaxation process is called the amplitude correlation time (τa). Specifically, the amplitude lifetime is the amount of time spent in the excited state before the molecule drops back to the final vibrational state; τa generally lasts a few picoseconds. The excited state lifetime directly affects the width of the Raman peak. If the molecule spends less time in the excited state, that will lead to a broader peak consistent with Heisenberg’s uncertainty principle.
Upon excitation, all the molecules vibrate coherently. However, molecular interaction and motion causes the ensemble of excited molecules to lose coherence. This process is called dephasing, and the time it takes for the molecules to lose coherence is called the coherence lifetime (τc). The coherence lifetime, like the amplitude correlation time, can also occur over several picoseconds. Together, these processes contribute to an overall effective lifetime of the molecules in the Raman scattering process. The process with the shortest lifetime will contribute the most to the spectral line shape.
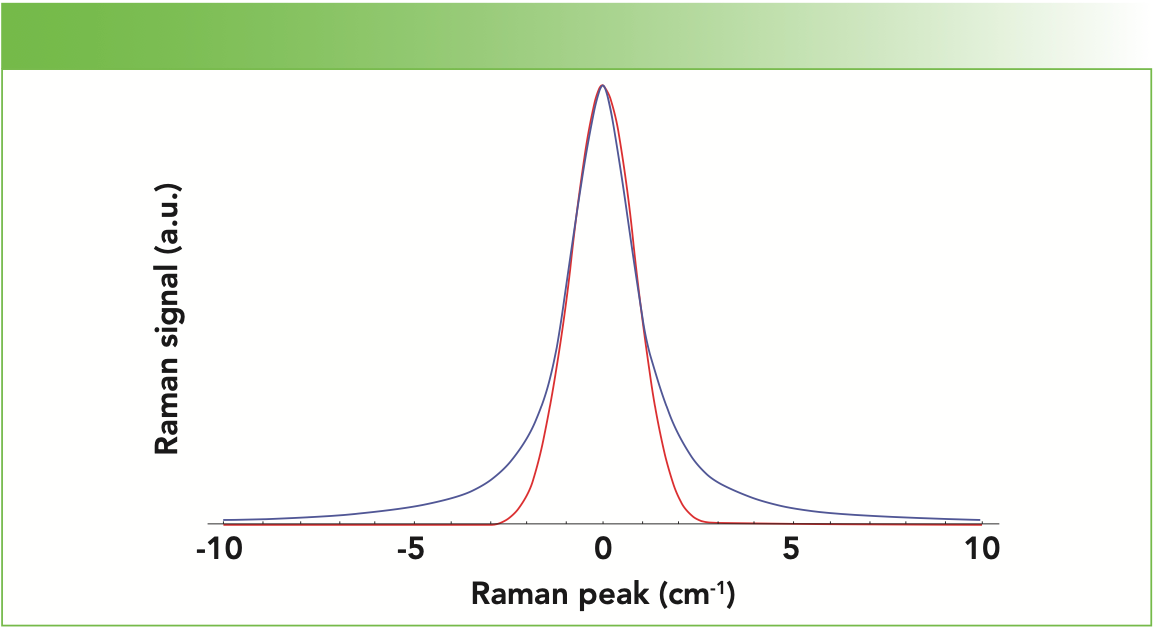
Let us then consider the contributing processes. If the coherence lifetime is much longer than the natural relaxation or amplitude correlation time (τc >> τa), then the molecules will relax before dephasing occurs. This condition generally applies to solids where the atoms or molecules hold relatively fixed positions. Consequently, the shapes of peaks in the Raman spectrum of a solid typically have Gaussian profiles that reflect the distribution of atomic positions and energy states in the solid. In contrast, gas molecules are in constant motion frequently undergoing collisions, and so dephasing can occur in gases much faster than the excited state relaxation (τc << τa). The dominant dephasing process leads to Raman spectra of gases with Lorentzian line shapes whose edges extend much further out than those of the Gaussian profile. See the normalized Gaussian and Lorentzian Raman peak profiles in Figure 1. The most significant differences between these line shapes appear below the full width at half-maximum (fwhm) of the peak. Here, you see a significant broadening of the edges of the Lorentzian profile compared to those of the Gaussian profile. Above the fwhm, the Gaussian and Lorentzian profiles differ only slightly.
FIGURE 1: Gaussian (red) and Lorentzian (blue) Raman peak profiles in arbitrary units: fwhm = 2 cm-1.
These cases shown in Figure 1 represent the idealized solid and gas phases of matter and their correlation to line shape. As you may expect, the liquid phase falls between the solid and gas phase limits. Consequently, the line shape of even an idealized liquid is best described by a percent contribution of Gaussian and Lorentzian character. Ultimately, all materials deviate from these idealized cases, and so that is why peak fitting often involves a percent contribution of Gaussian and Lorentzian character to produce the best fit to the observed peak.
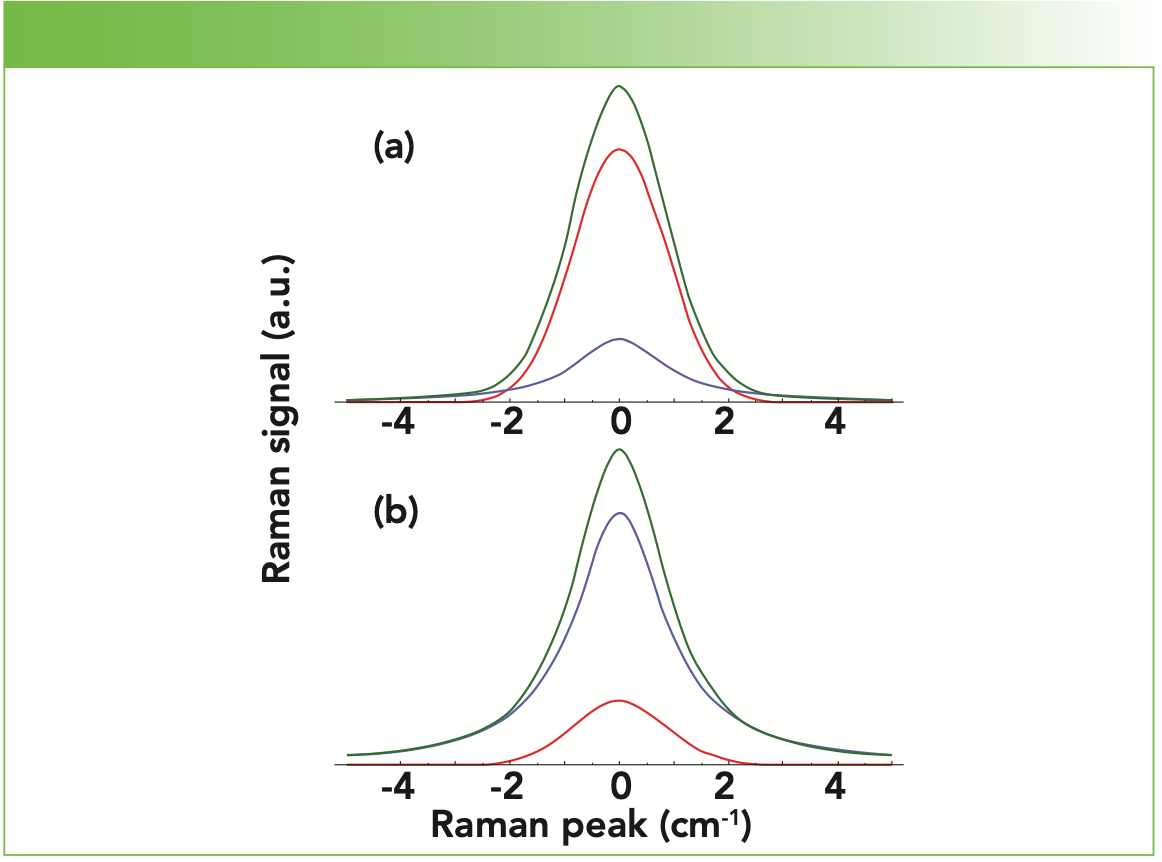
A demonstration of different contributions of Gaussian and Lorentzian character to a single peak shape is shown in Figure 2. An 80% Gaussian and 20% Lorentzian contribution to a single composite peak in Figure 2a yields a peak that looks primarily Gaussian in the center with only a slight extension of the peak edges below the fwhm of the peak. This is as one might expect from the low 20% Lorentzian contribution. Inverting these contributions to 20% Gaussian and 80% Lorentzian as shown in Figure 2b produces a slightly narrower composite peak above the fwhm. Also, the composite peak edges now extend beyond ± 2 cm-1 from the peak center such that the Lorentzian contribution and composite peak edges below the fwhm are nearly identical. Careful examination of Figures 1 and 2 should help you to understand the importance of incorporating the right mix of Gaussian and Lorentzian spectral line profiles to achieve the best peak fit to your acquired spectrum. Furthermore, the peak shapes and the percent Gaussian and Lorentzian contributions to the best fit provide information about excited state amplitude correlation and coherence lifetimes and molecular interactions involving specific vibrational modes.
FIGURE 2: Different Gaussian (red) and Lorentzian (blue) contributions to a single composite (green) peak: fwhm = 2 cm-1: (a) 80% Gaussian and 20% Lorentzian, and (b) 20% Gaussian and 80% Lorentzian.
Convolution of Two Closely Spaced Peaks
Now that we have discussed line shape profiles of single peaks, we can address another important application of peak fitting, which is characterizing closely spaced peaks that are not resolved experimentally. Again, our purpose here is not to teach the craft of peak fitting and use of peak fitting software. Rather, our goal is to help the reader visualize through peak modeling the effect of closely spaced peak convolution to better interpret Raman spectra and judge the reasonableness and underlying chemical and physical meaning of peak fitting results.
We start by considering two closely spaced 100% Gaussian peaks of different bandwidths separated by 2 cm-1, thereby generating a single asymmetric convolved peak. The central peak has a fwhm of 3 cm-1, whereas the side peak to the low wavenumber side has a fwhm of 2 cm-1. We simplify matters by modeling both peaks as 100% Gaussian so that one can readily observe the effect of the variable on the peak convolution. The variable, as seen in Figure 3, is the intensity of the side peak relative to that of the central peak set at 0 cm-1. The relative intensities of the side peak are 0.25, 0.50, 0.75, and 1.00. It is important to note that the two peak positions, bandwidths (fwhm), and their separation of 2 cm-1 remain fixed. Nevertheless, the changing relative intensity of the side peak produces initially a shift to lower wavenumber of the convolved peak maximum and then the emergence of a second maximum (partially resolved peak) as the relative intensity of the side peak increases.
FIGURE 3: Convolution (green) of two closely spaced Gaussian peaks of different bandwidths with the side peak (fwhm = 2 cm-1) (blue) varying in signal strength: (a) 0.25, (b) 0.50, (c) 0.75, and (d) 1.0, relative to that of the central peak (fwhm = 3 cm-1) (red).
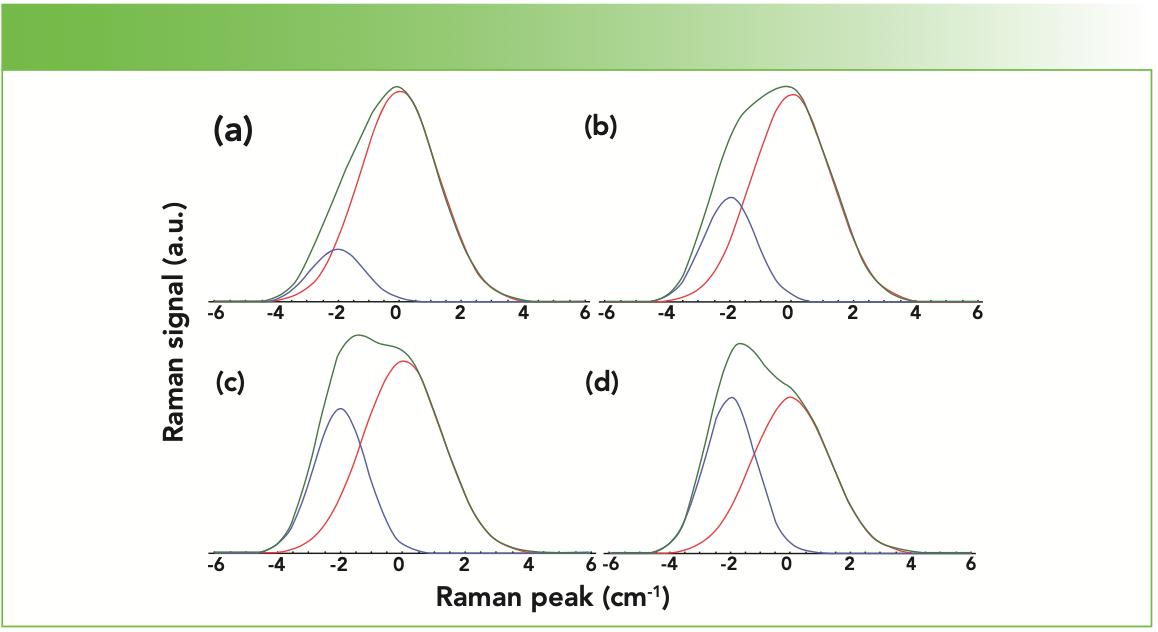
The important lesson to be learned here is that even though no change in the central and side peak positions has occurred, the change in relative intensities of two closely spaced peaks can give the appearance of peak shift if the two peaks are not spectrally resolved by the spectrometer. Hence, it is important to understand the effects of convolution of closely spaced peaks so as not to misinterpret a change in intensity of one or both contributing peaks as a shift of a single unresolved peak. Czarnecki has written an important paper on the origins of spectral changes caused by frequency shifts or intensity changes, and I encourage the interested reader to consult this publication (4).
It can be observed that the fwhms of the central and side peaks in Figure 3 are not the same. That choice was intentional and made for instructional purposes. If two closely spaced peaks each have a narrow bandwidth, they can be either completely or at least partially resolved. It is the broadening of each or both of the peaks’ bandwidth under convolution that leads to the emergence of a single convolved peak with shape and position that are not at all intuitive.
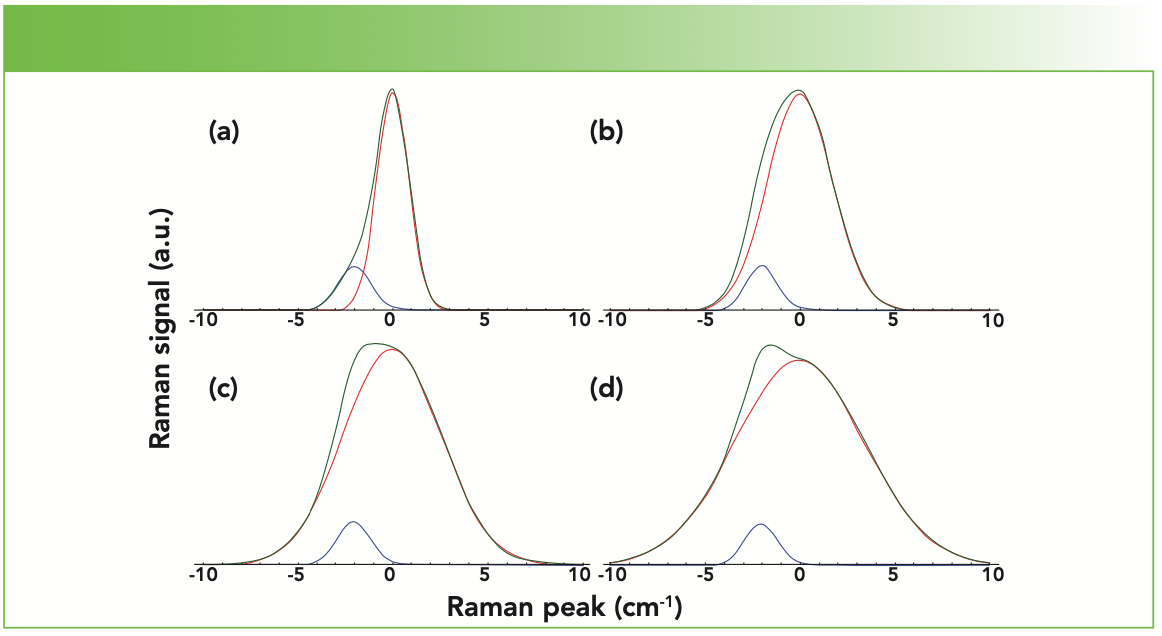
The nonintuitive effect of unresolved closely spaced peaks on convolved peak shape and position becomes abundantly clear when in our modeling, we vary the fwhm of the central peak while keeping the ratio of the side to central peak intensities at 0.2 and the peak separation fixed at 2 cm-1. The effect of varying only the fwhm of the central peak at 2, 4, 6, and 8 cm-1 is shown in Figure 4. At equal values of fwhm at 2 cm-1, an edge or tail below the fwhm emerges on the low wavenumber side of the convolved peak, whereas above the fwhm the peak ap- pears fairly symmetric. Next, we change the fwhm of the central peak to 4 cm-1 without making any changes to the posi- tion, intensity, or fwhm of the side peak, as seen in Figure 4b. Now, the low wave- number edge or tail of the convolved peak has vanished. The convolved peak appears broader, asymmetric, and its peak maximum appears shifted slightly to lower wavenumber. Increasing the fwhm of the central peak to 6 cm-1 in Figure 4c leads to a further broadening of the convolved peak with a flat top and a maximum that appears to be shifting to an even lower wavenumber. Finally, setting the fwhm of the central peak at 8 cm-1 in Figure 4d broadens the convolved peak further and produces a partially resolved maximum to the low wavenumber side of the central peak. To summarize, progressively increasing the bandwidth of the central peak has led to the emergence and partial resolution of the low wavenumber side peak. If one were only to see the progression of the convolved peak and not its components in Figure 4, the spectroscopist could easily attribute the changes to the intensity increase of the sideband even though that is not the true cause in this case.
FIGURE 4: Convolution (green) of two closely spaced Gaussian peaks with the side peak (blue) fixed at fwhm = 2 cm-1 and the central peak (red) varying in fwhm = (a) 2, (b) 4, (c) 6, and (d) 8 cm-1.
The effects on the convolved peak as a result of changing the central peak bandwidth are not at all intuitive, which is why modeling can be so helpful in understanding the effects of peak convolution. My hope is that by learning about peak shape and closely spaced peak convolution, you will be better prepared to assess the results of peak fit- ting tools. Those experienced with peak fitting software know that the results are not unique and can depend upon the initial settings of peak shape, position, and bandwidth. Ultimately, you want to be confident that the identified peaks have a reasonable chemical or physical basis when applied to your experimentally obtained Raman spectra.
Conclusion
To better understand spectral profiles, we briefly explained the physical basis of the so-called spectral line shapes. Furthermore, we discussed and modeled spectral line width and broadening to help the reader see how the percent of Gaussian and Lorentzian components contribute to overall peak shape and how two closely spaced and unresolved peaks of different amplitude or bandwidth can affect maximum position and the overall appearance of the convolved peak. Modeling the superposition of closely spaced peaks has been performed to help the reader visualize the effect of closely spaced peak convolution and so better interpret Raman spectra and judge the reasonableness and underlying chemical and physical meaning of peak fitting results.
References
(1) M.S. Bradley and C. Bratu, J. Chem. Educ. 74, 553–555 (1997).
(2) M.S. Bradley, Spectroscopy 30(11), 42–46 (2015).
(3) X. Yuan and R.A. Mayanovic, Appl. Spec. 71, 2325–2338 (2017).
(4) M.A. Czarnecki, Vib. Spec. 58, 193–198 (2012).
David Tuschel is a Raman Applications Scientist at Horiba Scientific, in Piscataway, New Jersey, where he works with Fran Adar. David is sharing authorship of this column with Fran. He can be reached at: SpectroscopyEdit@MMHGroup.com ●


AI-Powered SERS Spectroscopy Breakthrough Boosts Safety of Medicinal Food Products
April 16th 2025A new deep learning-enhanced spectroscopic platform—SERSome—developed by researchers in China and Finland, identifies medicinal and edible homologs (MEHs) with 98% accuracy. This innovation could revolutionize safety and quality control in the growing MEH market.
New Raman Spectroscopy Method Enhances Real-Time Monitoring Across Fermentation Processes
April 15th 2025Researchers at Delft University of Technology have developed a novel method using single compound spectra to enhance the transferability and accuracy of Raman spectroscopy models for real-time fermentation monitoring.
Nanometer-Scale Studies Using Tip Enhanced Raman Spectroscopy
February 8th 2013Volker Deckert, the winner of the 2013 Charles Mann Award, is advancing the use of tip enhanced Raman spectroscopy (TERS) to push the lateral resolution of vibrational spectroscopy well below the Abbe limit, to achieve single-molecule sensitivity. Because the tip can be moved with sub-nanometer precision, structural information with unmatched spatial resolution can be achieved without the need of specific labels.