A Training Set Sample Selection Method Based on SIMPLISMA for Robust Calibration in Near-Infrared Spectral Analysis

A training set sample selection method based on the simple-to-use interactive self-modeling mixture analysis (SIMPLISMA) algorithm is proposed in this article. We applied this method in near-infrared (NIR) spectral analysis of the content of protein, water, oil, and starch in corn. It is concluded that SIMPLISMA can be used as an alternative path to select training samples for constructing a robust prediction model in NIR spectral analysis.

In the field of quantitative analysis using near-infrared (NIR) spectroscopy, calibration is necessary. Training set sample selection is an important aspect of multivariate calibration, and it has attracted the attention of several researchers. The aim of this technique consists of the following two items:

• Choosing the smallest set of training samples that can be used without significantly compromising the prediction performance of the model. It is often used to save computational work (1–8). In some situations, the representative samples used in multivariate calibration can benefit both the modeling efficiency and the prediction performance.

• Training set sample selection is also an important part in the context of transfer of multivariate calibration models (9–11), in which a subset of samples must be measured in different spectrometers. The measurements are then used to standardize the instrumental response of one or more spectrometers (slaves) with respect to a single one (master). In this case, a small number of representative samples are chosen so that they will contain sufficient information about the variations of the samples because of different measurement conditions. This benefits the practical application.

In this article, we mainly discuss the first case, which involves the training set sample selection method and subset selection from full calibration samples. A sufficient number of samples with a wide concentration (or the nature) distribution of the analyte is needed for constructing a calibration model. Especially during the selection of the representative training samples, it is helpful for us to establish a calibration model with higher efficiency and good accuracy.

Several works have discussed the problem of selecting a representative subset from a large pool of samples (1,2,12–14). In general, there are three types of training set sample selection methods: random sampling; sample selection based on data analysis of instrumental response variables x (that is, spectra); and sample selection based on data analysis of instrumental response variables x and output vector y (that is, concentration or the nature of the analyte).

Random sampling is the most popularly used method because of its simplicity — a group of data randomly extracted from a larger set follows the statistical distribution of the entire set. However, random sampling does not guarantee that representative samples are included in the calibration, and it also does not ensure that the samples on the boundaries of the set are selected in the calibration.

Therefore, many sample selection methods based on data analysis of instrumental response variables x are typically used; an example would be the linear algebra techniques similar to spectral subtraction proposed by Honigs (12), or the Kennard–Stone (KS) algorithm, which is an alternative that is often used. KS is aimed at covering the multidimensional space in a uniform manner by maximizing the Euclidean distances between the instrumental response vectors (x) of the selected samples (13,14). The advantage of the KS algorithm is that it ensures that the selected samples are uniformly distributed in accordance with the spatial distance. Despite the comparative advantages of KS, however, the data conversion and the space distance between samples must be calculated, which is a challenging computation procedure. Another shortcoming of the KS algorithm for multivariate calibration lies in the fact that the statistics of the output vectors (y) are not taken into account (2).

Recently, some studies of sample selection have focused on the data analysis of instrumental response variables x and output vector y (1,2). It could be argued that the inclusion of y-information in the selection process might result in a more effective distribution of calibration samples in the multidimensional space, thus improving the predictive ability and robustness of the resulting model. In the work of Galvão and colleagues (1), an approach for considering joint x–y statistics in the selection of samples is proposed for the purpose of diesel analysis by NIR spectrometry. The method, termed sample set partitioning based on joint x–y distances (SPXY), extends the KS algorithm by encompassing both x- and y-differences in the calculation of inter-sample distances. In other words, in comparison to KS, the y-information is considered by SPXY. However, the collinearity effect between samples is not included in the algorithm. Especially when hundreds of samples are used in calibration, the collinearity effect exists.

In this article, we extend the simple-to-use interactive self-modeling mixture analysis (SIMPLISMA) method as a novel, training set, sample selection method for eliminating samples with collinearity. In this method, x and y-information are included in the sample selection process. The selected representative samples for calibration are used to improve the modeling efficiency, and good accuracy can be achieved.

SIMPLISMA was originally developed by Willem Windig and colleagues for pure variable selection (15). A pure variable is defined as a variable whose intensity mainly results from one of the components in the mixture under consideration (16). According to the purity spectrum and standard deviation spectrum of variables, the pure variables can be selected straightforwardly. And the determinant-based function is used in SIMPLISMA for determining the independence of variables. The point is to eliminate collinearity of variables.

SIMPLISMA has been successfully used for the investigation of peak purity with liquid chromatography (LC) and diode-array detection (DAD) data (17). It also has been applied for the second-derivative NIR spectra to resolve highly overlapping signals with a baseline problem (18). Also, SIMPLISMA has already been applied to the analysis of categorized pyrolysis mass spectra data, Fourier transform infrared (FT-IR) spectroscopy, microscopy data of a polymer laminate, Raman spectra of a reaction followed in time, and so on (19–22).

This article discusses the use of SIMPLISMA for the selection of samples for a training set for multivariate calibration in NIR spectral analysis. In this study, SIMPLISMA is used to select a subset of calibration samples that are minimally redundant but still representative of the data set. It is not the same as pure variable selection by SIMPLISMA; this approach involves pure sample selection using the SIMPLISMA principle to eliminate the collinearity of samples. Our goal is to reduce computational work and obtain a robust multivariate model with stable prediction performance. The sample selection method takes into account both x and y statistics by combining with wavelength-variable selection, which is helpful in resolving multicomponent chemical or physical information of the mixture from overlapped spectra. The use of SIMPLISMA for sample selection is illustrated for NIR spectra analysis of the protein, water, oil, and starch content in corn. In this application, sample selection by SIMPLISMA is also compared to the KS algorithm and the SPXY method.

Materials and Methods

The corn data (http://www.eigenvector.com/data/Corn/index.html) used in our study consists of 80 samples of corn measured on three different NIR spectrometers (named m5, mp5, and mp6). In our study, the spectra from instrument m5 are used. The wavelength range is 1100–2498 nm, and the number of wavelength variables is 700. There are four output variables (the content of protein, moisture, oil, and starch).

To determine the quality of the corn data used in our work, we first tested the potential sample outliers using principal component analysis (PCA).

Then, for each output variable, 20 samples were selected randomly as an independent external prediction set for evaluating the prediction performance of the calibration model, and the remaining 60 samples were used for calibration. As a result, four calibration sets and the corresponding prediction sets are assembled in this study for spectra analysis of the four components in corn, respectively.

The aim of this experiment is to choose a small quantity of representative samples from the 60 samples (the dimension of original spectra matrix is 60 × 700). Then the selected training samples are used for building partial least squares (PLS) models, which are used for predicting the protein, moisture, oil, and starch content. To make the spectra matrix correlate with each analyte, a wavelength-variable selection method — a successive projections algorithm (SPA) — was used before the training set sample selection. SPA is a forward selection method in that it starts with one wavelength and then incorporates a new one at each iteration. The new wavelength is selected according to a sequence of projection operations, until a specified number N of wavelengths is reached. Its purpose is to select wavelengths whose information content is minimally redundant, and to solve collinearity problems (23). In the SPA wavelength-variable selection process, there are four different wavelength-variable sets for quantitative analysis of the content of protein, moisture, oil, and starch, respectively. It is possible to make the new matrices with selected variables and selected samples correlate with the corresponding components' information. Using the variable selection method based on SPA, we can easily extract the most relevant spectral information of a component from the overlapped NIR spectrum. Moreover, the application of wavelength selection benefits SIMPLISMA by selecting training samples that are associated with the analyte in consideration. That means sample selection takes into account both x and y statistics, which is useful for improving prediction performance.

Thereafter, two training set sample selection methods, KS and SPXY, were introduced in this study for comparison with the proposed method based on SIMPLISMA. PLS models were built by using training samples, which were selected by different training set sample selection methods. Leave-one-out cross-validation (LOO-CV) applied to the training set was used to select the principal components. The prediction performance of the PLS models were evaluated according to the root mean squares error of calibration (RMSEC) set and root mean squares error of prediction (RMSEP) set. Root mean squares error (RMSE) is calculated as follows:

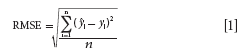
where ŷ_i is prediction value, y_i is reference value, and n is the number of samples.

The algorithms of PCA, SPA, PLS, SIMPLISMA, KS, and SPXY were all performed using Matlab 7.6.0 (The Mathworks, Inc.).

Training Set Sample Selection Algorithms

KS Algorithm

The classic KS algorithm is targeted at selecting a representative subset from full calibration samples. To ensure a uniform distribution of such a subset along the x (instrumental response) data space, the KS algorithm follows a stepwise procedure in which new selections are taken in regions of the space far from the samples already selected (2). The algorithm is described as follows.

Step 1

Initialization of the number of the samples proposed to be selected by the analyst.

Step 2

Calculate the Euclidean distances d_x (p, q) of each pair (p, q) of samples; the calculation equation is as follows:

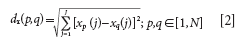
For spectral data, x_p (j) and x_q (j) are the instrumental responses at the jth wavelength for samples p and q, respectively. J denotes the number of wavelengths in the spectra. N is the number of the original full calibration samples.

Step 3

According to the results calculated by equation 2, selecting the pair (p₁, p₂) of samples for which the distance d_x (p₁, p₂) is the largest.

Step 4

Calculate the distances between each remaining sample and the two selected samples. For the remaining samples, these distances are the smallest distance to the selected samples. Then, select the sample for which the distance is the largest as the third sample.

Step 5

Repeat step 4 until the number of samples specified in step 1 by the analyst is achieved.

SPXY Algorithm

We can see that, under the KS algorithm, only the x information is involved in consideration for sample selection. The SPXY algorithm proposed by Galvão in 2005 (2) is based on KS; the difference is that the information about output variable y is involved in the calculation of distance. Such a distance d_y (p, q) can be calculated for each pair of samples p and q as

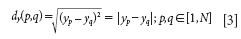
To assign equal importance to the distribution of the samples in the x and y spaces, distances d_x (p, q) and d_y (p, q) are divided by their maximum values in the data set. In this manner, a normalized xy distance is calculated as

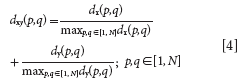
This stepwise selection procedure is similar to the KS algorithm; the difference is that the distance calculation is based on d_xy (p, q) instead of just d_x (p, q).

Originally, the SPXY method was proposed for calibration and validation subset partitioning. In this article, we introduce this method for training set sample selection and compare the performance of different sample selection methods.

SIMPLISMA Algorithm

KS and SPXY algorithms are based on the calculation of Euclidean distances. In this study, based on the SIMPLISMA theory, we used the pure values calculation for elimination of collinearity among samples, and then selected a sample subset with minimal redundant information for calibration. The SIMPLISMA algorithm for training set sample selection is described as follows:

Step 1: Selecting the First Sample

Initially, the basis of SIMPLISMA is to determine the purity. In this approach, SIMPLISMA is used to calculate the purity of samples for determining the first sample. In this article, the data matrix is represented by X, and the size is n × m, where n is the number of samples and m is the number of wavelength variables. Because we have selected wavelength variables using SPA before sample selection, m is the number of wavelength variables after the wavelength selection step has been executed. The purity value of sample i is calculated as

where σ_i is the standard deviation and µ_i is the mean. The constant α is added to the denominator to avoid the problem from noise-level mean value of samples. Typical values for α range from 1% to 5% of the maximum of µ_i. The index 1 represents the first sample that will be selected. According to the purity spectrum of the samples, the sample with the highest intensity is selected as the first informative sample, which will be used in calibration later.

Step 2: Selecting the jth Samples (j ≥ 2)

The problem now is how to eliminate collinearity among samples and how to determine the next informative sample for calibration. The jth sample is the one that is the most independent to the (j - 1)th sample selected. So, it is possible to determine correlation weight by the determinant-based function p_i,j (15,24,25), which is used for correcting the previous purity value of selected samples. The determinant-based function is calculated as described below.

The correlation around the origin (COO) matrix needs to be calculated first. The COO dispersion matrix is used for giving all the samples an equal contribution in the calculation. The COO matrix is

Where

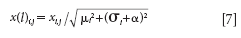
Equation 7 is used for scaling the data matrix.

Then, the determinant (equation 8) is calculated for selecting sample j and j ≥ 2.

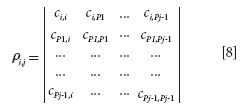
where p_j-1 represents the index of the (j - 1)th selected sample in the COO matrix. If sample i is highly correlated with the previously selected sample (j - 1), the value for ρ_{i, j} is close to 0; if sample i is dissimilar to the previously selected sample (j - 1), the value for ρ_{i, j} is high. The values of the determinants can be used to determine the next samples.

The next samples can be selected by the following purity spectrum with a weight function ρ_{i, j}:

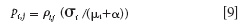
Therefore, the sample i with the maximum value of ρ_{i, j} is selected as the jth informative sample, which will subsequently be used in calibration.

Step 3: Determination of the Number of Samples

How many representative training samples are needed for calibration? To have a parsimonious PLS model, we hope to select minimal number of samples. Meanwhile, the model displays no significant loss of prediction accuracy. However, there are no uniform methods to determine the number of training samples. Here, we introduce the RMSEP of COO-CV as a target function for determining the optimal number of samples. It is also an empirical approach, so intuitive sense and visual judgment of the purity of samples are useful for us to make the decision.

Figure 1: PCA score plot for analysis of outliers in corn samples. The potential outliers are marked by black solid circle and sample index.

Results and Discussion

Sample Outliers Testing and Discussion

According to the theory of SIMPLISMA, we can see that if a sample outlier has the largest value of p_i,j, it will be mistaken as an informative sample, and thus the sample selection method based on SIMPLISMA is invalid. So, outliers should be excluded in advance when using SIMPLISMA for training set sample selection. Therefore, we first tested for sample outliers in the corn data. The traditional PCA method is introduced in reference 26, and the score scatter plot of the first principal component and the second principal component is given in Figure 1. In Figure 1, the score distribution information for the original 80 samples is given. Several potential outliers are marked by solid black circles and sample index (46,68,72,75,77). According to Davies (26), a sample that is on the edge of the population in a scatter plot may be not an outlier, and we only need to remove samples that have an obvious problem. So, the potential outliers may be not outliers even though we have also tested these potential sample outliers by cross-validation. Table I shows the PLS calibration exercise results of moisture content. In fact, other components results are similar. It is concluded that these possible outliers do not have a great influence on the model with the full samples. Therefore, we have reason to believe that there are no obvious sample outliers in our experimental data and all the data are used in this work.

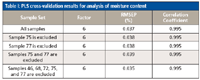
Table I: PLS cross-validation results for analysis of moisture content

Wavelength Variable Selection Results by SPA

Before the selection of training samples, SPA is first applied to the four calibration sets randomly reassembled for spectral analysis of the four components in corn. Thus, four new matrices are constructed, and each matrix is correlated with the corresponding analyte. For spectral analysis of protein, the number of wavelength variables is reduced from 700 to 57. For spectral analysis of moisture, the number of wavelength variables is reduced from 700 to 24. For spectral analysis of oil, the number of wavelength variables is reduced from 700 to 35. And for spectral analysis of starch, the number of wavelength variables is reduced from 700 to 57. Figure 2 shows the results of wavelength-variable selection by SPA for the four components: protein (+), moisture (*), oil (x), and starch (o). Among the selected variables for spectral analysis of protein, the wavelengths of 1460, 1492, 1508, 1524, 2152, and 2186 nm were selected, which were in the characteristic bands of 1460–1492 nm, 1500–1530 nm, and 2148–2200 nm. According to the wavelength-variable selection results for spectral analysis of moisture, two characteristic peaks (around 1500 nm and 2080 nm) were selected by SPA. And for spectral analysis of starch, two characteristic peaks (close to 2500 nm and 1490 nm) were selected by SPA, and three wavelength variables (2306 nm, 2284 nm, and 2290 nm) in the characteristic band of 2280–2330 nm were selected. According to the wavelength-variable selection results for spectral analysis of oil, there were two characteristic peaks (2140 nm and 2470 nm) selected by SPA. It is clear that the distributions of the selected variables for the four components are very different. It is implied that wavelength-variable selection is useful for resolving concentration information of different components in a mixture simultaneously.

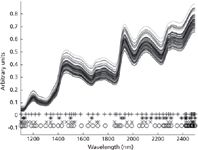
Figure 2: Wavelength variables selected by SPA for spectra analysis of the four components: protein (+), moisture (*), oil (x), and starch (o).

Next, the PLS models were obtained by using the selected wavelength variables. The models were utilized to predict the external independent prediction sets. The prediction parameters are shown in Table II. For comparison, the prediction results obtained by PLS models with all 700 variables are also presented. The results indicate that, under the variable selection of SPA, for quantitative analysis of protein, moisture, and oil, the prediction accuracy is close to the PLS model built with full variables. For quantitative analysis of starch content, despite the RMSEP for the selected-wavelength model (0.340%), it was slightly larger than the RMSEP for the full-wavelength model (0.322%), but there is no significant loss of the model accuracy. Moreover, SPA is helpful for us to improve modeling efficiency when we only use a small amount of samples for modeling. On the other hand, it is implied that the selected variable subset belongs to the corresponding analyte, which makes the relation between x and y closer. It also indicates that wavelength-variable selection is useful for us to resolve concentration information for different components in the mixture simultaneously from overlapped NIR spectra.

Table II: Prediction results for protein, moisture, oil, and starch content

Sample Selection Results by SIMPLISMA

Under the wavelength-variable selection based on SPA, there are four new matrices reconstructed for the quantitative analysis of protein, water, oil, and starch content in corn, respectively. To obtain a more parsimonious PLS regression model with good prediction performance, SIMPLISMA was used to select representative training samples from the original 60 calibration samples, and we set the noise level a at 5% of the maximum mean value of all the samples.

For spectral analysis of protein content, the number of calibration samples was reduced from 60 to 47 by training set sample selection based on SIMPLISMA. It can be seen that the modeling problem is simplified because the matrix dimension was reduced from 60 × 700 to 47 × 57. The new matrix obtained by variable selection and sample selection was used in the PLS model and the external, independent prediction set was introduced to evaluate the prediction performance of the parsimonious PLS model. The prediction results are presented in Table III. The RMSEP values are 0.143% and 0.140% for the PLS model built by all calibration samples and the PLS model built by selected training samples, respectively. It is clear that both models have similar prediction accuracy. It is implied that, under the sample selection strategy, the parsimonious PLS model has good robustness, which has similar prediction accuracy with full-sample model.

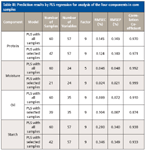
Table III: Prediction results by PLS regression for analysis of the four components in corn samples

For spectral analysis of moisture content, SIMPLISMA selected 21 training samples from the original 60 calibration samples. The prediction ability of the resulting PLS model was assessed in terms of RMSEP of the external independent prediction set. As shown in Table III, the reduction in the number of calibration samples does not compromise the prediction performance of the PLS model. In contrast, the RMSEP was decreased from 0.048% to 0.021%. In this application, it is indicated that optimizing the training set used in PLS is useful for improving prediction accuracy.

The same process was followed for the spectral analysis of protein and moisture content; under the training sample selection method based on SIMPLISMA, there are 39 and 42 training samples selected from original 60 calibration samples for quantitative analysis of oil and starch, respectively. The external independent prediction set was used for evaluating the resulting PLS models. As shown in Table III, for spectral analysis of oil content, the RMSEP is 0.072% and 0.087% for the PLS model built by all calibration samples and the PLS model built by selected training samples, respectively. For spectral analysis of starch content, the RMSEP is 0.340% and 0.349% for the PLS model with full samples and the PLS model with selected samples, respectively. There are no significant losses of the model accuracy when we only use a smaller amount of samples for modeling. That is, the reduction in the number of calibration samples does not compromise the prediction accuracy of the full-sample model. Moreover, modeling efficiency is improved by the sample selection process. The multivariate calibration models constructed by the training samples selected based on SIMPLISMA have good linearity.

Figure 3: Three-dimensional PLS score plot for NIR spectral analysis of four components in corn: (a) protein, (b) moisture, (c) oil, and (d) starch. The samples selected by SIMPLISMA are highlighted by circles.

Besides the prediction error, there was other evidence to corroborate the validity of the proposed training set sample selection method based on SIMPLISMA. Figure 3 shows that the selected samples are well spread in the X-space (as projected in the three-dimensional space of PC1-PC2-PC3 scores, where PC1 is the first principal component, PC2 is the second principal component, and PC3 is the third principal component). We can see that the selected samples are dispersed in the full sample space. It is implied that a representational training set can be obtained by SIMPLISMA. As shown in Figure 4, the + symbol indicates the selection of a sample with corresponding content. The denseness of the distribution of the + symbol indicates the selected frequency of sample with corresponding content. That is, the denser the distribution of the + symbol, the more samples with certain content are selected. So, Figure 4 shows that the protein, moisture, oil, and starch of the selected samples are all well spread across the range found in the entire data set. These findings indicate that SIMPLISMA takes into account both x (spectra) and y (analyte content) information to tailor the selection to the chemical species involved in the analysis. This suggests that the structure of the x-y relationship is effectively captured by the selected samples.

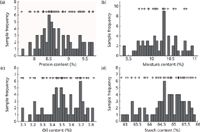
Figure 4: Samples frequencies distribution of different contents for the four components in corn samples: (a) protein, (b) moisture, (c) oil, and (d) starch. The selected 47, 21, 39, and 42 samples for analysis of the four components are respectively indicated on top of the corresponding histogram bins by the + sign.

Comparison of KS, SPXY, and SIMPLISMA

In this study, the SIMPLISMA method was compared with two classic methods (KS and SPXY) for training set sample selection. Similarly, before performing training set sample selection, the variable selection based on SPA was done first. The three kinds of training set sample selection methods were used to construct the PLS models built by selected variables and selected samples. The results are shown in Table IV. It is clear that, for the NIR spectral analysis of protein content in the corn samples, the SIMPLISMA-PLS model has the best result (RMSEP is 0.140%). For the NIR spectral analysis of moisture and oil content, the RMSEP values of SIMPLISMA-PLS (0.021% and 0.087% for moisture and oil, respectively) are not better than that of the KS-PLS model (0.018% and 0.077% for moisture and oil, respectively), but those are better than SPXY-PLS (0.029% and 0.094%, respectively). For the NIR spectral analysis of starch content, the RMSEP of SIMPLISMA-PLS (0.349%) is the lowest, but the prediction accuracy difference is smaller when compared with the two models (KS-PLS and SPXY-PLS). It is very encouraging that a robust multivariate calibration model can be constructed by training samples selected based on SIMPLISMA, despite the fact that there are negligible differences between the results. In our opinion, the fact that SIMPLISMA provides an alternative training set sample selection method has practical significance. It can be used for selecting a smaller amount of samples representing the information of the original full-sample set, displays no compromise for the model accuracy, and greatly improves the modeling efficiency.

Table IV: Comparison of prediction performance of SIMPLISMA-PLS, KS-PLS and SPXY-PLS models for NIR spectra analysis of protein, moisture, oil, and starch content in the corn samples

Conclusions

SIMPLISMA was originally intended as a pure variable selection technology. It was extended in this study for the selection of training samples for multivariate modeling. It is developed here for selecting a subset of samples that are minimally redundant, but still representative of the original data set, and the aim is to improve prediction performance and modeling efficiency for getting a robust multivariate calibration model. The corn data was introduced in this study to evaluate the proposed training set sample selection method based on SIMPLISMA. It is concluded that

• The sample selection strategy based on SIMPLISMA includes a wavelength selection method, such as SPA introduced in this article. That is, SIMPLISMA is followed by wavelength selection of SPA. There are four matrices for spectra analysis of protein, moisture, oil, and starch content in the corn samples that were reconstructed by SPA. Thus, each matrix is related to the corresponding analyte. It is the main reason that both x and y statistics can be considered in the training set sample selection method based on SIMPLISMA.

• Under the SIMPLISMA theory, the sample with the maximum purity is selected and the weight function added in the purity value calculation is used for eliminating collinearity among samples. Thus, a small set of calibration samples with minimum collinearity is determined that is still representative of the original data set. For the NIR spectral analysis of protein, water, oil, and starch content in the corn samples, the SIMPLISMA strategy provides a reduction in the number of samples from 60 to 47, 21, 39, and 42, respectively. There is no significant compromise in the prediction ability of the full-sample PLS models.

• In this application, SIMPLISMA is compared with the classical sample selection methods such as KS and SPXY that are introduced in this article. The results indicate that, SIMPLISMA-PLS models have similar results to the KS-PLS and SPXY-PLS models. It is encouraging that the SIMPLISMA method can be used as an alternative path to select representative training samples for constructing a robust prediction model with good accuracy in NIR spectral analysis, which is helpful to improve modeling efficiency.

In the training set sample selection based on SIMPLISMA (especially for the multicomponent analysis using NIR spectroscopy such as NIR spectral analysis of the four components content in corn in this paper), the SPA wavelength-variable selection method is used before SIMPLISMA for resolving multicomponent chemical or physical information of complex mixture simultaneously from overlapped NIR spectra, which helps SIMPLISMA select samples more representatively for the four respective components. In addition, SIMPLISMA is not sensitive to outliers with gross errors, so outliers should be excluded in advance when using SIMPLISMA for training set sample selection.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 51205140) and the Scientific Research Fund Project of Huaqiao University (No. 11BS413).

References

(1) H.A.D. Filhoa, R.K.H. Galvão, M.C.U. Araújo, E.C. da Silva, T.C.B. Saldanha, G.E. José, C. Pasquini, I.M.R., Jr., and J.J.R. Rohwedder, Chemom. Intell. Lab. Syst. 72, 83–91 (2004).

(2) R.K.H. Galvão, M.C.U. Araújo, G.E. José, M.J.C. Pontes, E.C. da Silva, and T.C.B. Saldanha, Talanta 67, 736–740 (2005).

(3) J.F. Magallanes, J. of Chemometrics 23, 132–138 (2009).

(4) F.A. Iñón, J.M. Garrigues, S. Garrigues, A. Molina, and M. de la Guardia, Anal. Chim. Acta489, 59–75 (2003).

(5) Y.D. Wang, D.J. Veltkamp, and B.R. Kowalski, Anal. Chem. 63, 2750–2756 (1991).

(6) E. Bouveresse and D.L. Massart, Chemom. Intell. Lab. Syst. 32, 201–213 (1996).

(7) F. Navarro-Villoslada, L.V. Pérez-Arribas, M.E. Leon-Gonázlez, and L.M. Pólo-Díez, Anal. Chim. Acta 313, 93–101 (1995).

(8) J. Ferré and F. Xavier-Rius, Trends Anal. Chem. 16, 70–73 (1997).

(9) R.N. Feudale, N.A. Woody, H. Tan, A.J. Myles, S.D. Brown, and J. Ferré, Chemom. Intell. Lab. Syst. 64, 181–192 (2002).

(10) F.A. Honorato, R.K.H. Galvão, M.F. Pimentel, B. de B. Neto, M.C.U. Araújo, and F.R. de Carvalho, Chemom. Intell. Lab. Syst.76, 65–72 (2005).

(11) J.L.P. Pavón, M. del N. Sánchez, C.G. Pinto, M.E.F. Laespada, and B.M. Cordero, Anal. Chem. 75, 6361–6367 (2003).

(12) D.E. Honigs, G.M. Hieftje, H.L. Mark, and T.B. Hirschfeld, Anal. Chem. 57, 2299–2303 (1985).

(13) W. Wu, B. Walczak, D.L. Massart, S. Heuerding, F. Erni, I.R. Last, and K.A. Prebble, Chemometr. Intell. Lab. Syst. 33, 35–46 (1996).

(14) K.R. Kanduc, J. Zupan, and N. Majcen, Chemometr. Intell. Lab. Syst. 65, 221–229 (2003).

(15) W. Windig and J. Guilment, Anal. Chem. 63, 1425–1432 (1991).

(16) R. Gargallo, R. Tauler, F. Cuesta-Sánchez, and D.L. Massart, Trends Anal. Chem. 15, 279–286 (1996).

(17) F. Cuesta-Sánchez, and D.L. Massart, Anal. Chim. Acta 298, 331–339 (1994).

(18) W. Windig and D.A. Stephenson, Anal. Chem. 64, 2735–2742 (1992).

(19) W. Windig, C.E. Heckler, F.A. Agblevor, and R.J. Evans, Chemom. Intell. Lab. Syst. 14, 195–207 (1992).

(20) W. Windig, and S. Markel, J. Mol. Struct. 292, 161–170 (1993).

(21) W. Windig, Chemom. Intell. Lab. Syst. 36, 3–16 (1997).

(22) W. Windig, D.E. Margevich, and W.P. McKenna, Chemom. Intell. Lab. Syst. 28, 109–128 (1995).

(23) M.C.U. Araújo, T.C.B. Saldanha, R.K.H. Galvão, T. Yoneyama, H.C. Chame, and V. Visani, Chemom. Intell. Lab. Syst. 57, 65–73 (2001).

(24) E.R. Malinowski, Anal. Chim. Acta 134, 129–137 (1982).

(25) K.J. Schostack and E.R. Malinowski, Chemom. Intell. Lab. Syst. 6, 21–29 (1989).

(26) A.M.C. Davies, Spectrosc. Eur. 18, 23–24 (2006).

Lina Li, Tianliang Lin, and Rencheng Zhang are with the Department of Detection and Control Engineering at Huaqiao University in China. Direct correspondence to: lilina@hqu.edu.cn.