Analysis of Infrared and Raman Imaging Data Using Alternating and Modified Alternating Least Squares

Modified alternating least squares (MALS) outperforms alternating least squares (ALS) in the analysis of infrared and Raman image spectral data. MALS offers superior stability thanks to ridge regression and a substantial speed advantage due to the kernel nature of the algorithm, reducing computational overhead. MALS excels in resolving basis vectors even in low signal-to-noise, nearly collinear data, whereas ALS often falls short. For spectroscopic imaging, both MALS and other ALS methods rely on spatial resolution between sample components, as low spatial resolution leads to increased mixing of components. Spectroscopic imaging combines spectroscopy and digital imaging to extract chemical composition. Multivariate curve resolution (MCR)’s foundation in ALS regression makes it a vital tool for this analysis, enabling a comprehensive examination of complex spectroscopic images. This tutorial delves into the mathematical techniques necessary for extracting chemical insights from infrared and Raman spectroscopic images. While this discussion focuses on two-dimensional spatial data, the methodology can be extended to three-dimensional data.

Spectroscopic imaging combines spectroscopic techniques such as infrared and Raman spectroscopy with digital imaging to obtain the chemical composition of a sample—for example, an emulsion (1) or an automotive paint chip (2), whose constituents lie in localized and distinct regions of the sample. The ability to mathematically resolve and analyze the chemical information contained in these samples depends on both spatial and spectral specificity and selectivity. Although spectroscopic imaging is not limited to microscale samples, most imaging studies are performed using a microscope to achieve optimal spatial resolution of the sample image. The spatially resolved spectra are collected and arranged in a data matrix where each row of the matrix is a spatially resolved spectrum. Whether the sample is moved sequentially along the x-dimension or along the x and y dimensions into the beam of the microscope by rastering (if a motorized stage and mapping software are available) or whether an image of the sample is focused onto an array detector, the spectra collected are treated in the same way, as the inherent data structure is the same. This tutorial focuses on the mathematics used to extract chemical information from Raman and infrared spectroscopic images. Although several reviews (3,4), book chapters (5,6), and books (7,8) have been published on this subject, this tutorial will enumerate current practices in the field of infrared and Raman image analysis.

A typical infrared and Raman image dataset consists of a spectrum associated with each (x, y) spatial dimension. Although the data suggest a three-dimensional problem, numerically the problem is two-dimensional, as the spatial dimensions are correlated and spatial information is not used in the solution to the problem. Furthermore, imaging data can be collected as a spectrum at each point in three spatial dimensions; however, the solution reduces to a two-dimensional problem. The two-dimensional spatial case will be the subject of this tutorial. However, the methodology discussed in this article can be readily extrapolated to three-dimensional spatial data.

Multivariate Curve Resolution

An important software tool used to extract and analyze information from infrared and Raman spectral image data is multivariate (self-modeling) curve resolution. The heart of multivariate curve resolution (MCR) is alternating least squares (ALS) regression (9,10). ALS is currently the most widely used method to solve infrared and Raman spectral image analysis problems. As opposed to traditional approaches which are restricted to partial visualization and analysis of the data, ALS utilizes the entire measurement.

The starting point for understanding ALS is principal component analysis (PCA) (11). The number of chemical components comprising the sample is determined by estimating the rank of the data matrix representing the image, which can be accomplished by decomposing the data matrix into a score matrix (designated by C in equation 1), loading matrix (designated by S in equation 1), and residual matrix (designated by E in equation 1), with the rank equal to the number of significant principal components present in the data (see equation 1, where t is the number of infrared [IR] or Raman spectra collected over the image, w is the number of wavelengths in each spectrum, and p is the number of components comprising the sample). Determining the number of significant principal components (such as, for example, the number of chemical components) is often a problem because of accidental correlations between signal and noise. Furthermore, PCA constitutes a purely mathematical solution which is often devoid of physical or chemical meaning because there are more wavelengths than constituents. The solution to both problems is the development of a suitable rotation.

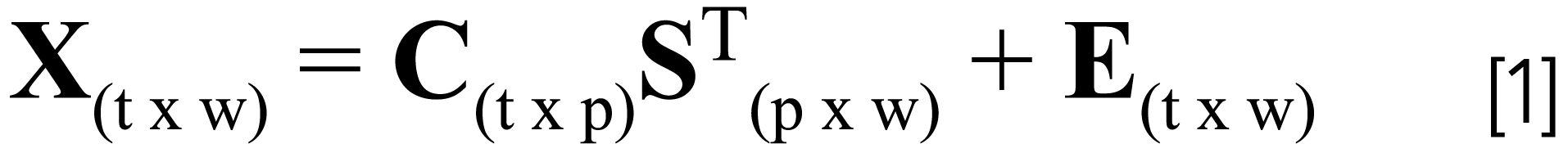
ALS transforms the score and loading matrices more meaningfully by seeking a rigorous algebraic solution to the problem of estimating the factors that best reconstruct the data matrix. To facilitate accuracy, both a non-negativity constraint and a unimodality constraint can be applied to both the score and loading matrices. The non-negativity constraint forces the elements of both the score and loading matrix to be greater than or equal to zero. Applying this constraint is logical since both absorbance and concentration cannot be less than zero. A unimodality constraint can also be applied to the score matrix to facilitate the identification of regions in the spectral image that correspond to spectra enriched with one of the components comprising the sample. However, the unimodality constraint should only be imposed when each sample component has a peak shaped concentration profile with a single maximum.

ALS decomposes a data matrix (image slice), X, into three matrices (see equation 1), where C contains the concentration profile of each sample component and S contains the spectral profile of each component. Equation 1 is solved iteratively using equations 2 and 3. To perform ALS, an initial estimate of C must be provided by the user, and S is then computed (see equation 2). The computed value of S is used to obtain an improved estimate of C. From the product of C and S, an estimate of the PCA-reproduced data matrix, X_PCA, is calculated. This process is repeated until convergence is achieved. To facilitate convergence, constraints such as nonnegative absorbance and concentration and unimodality are applied to the data.

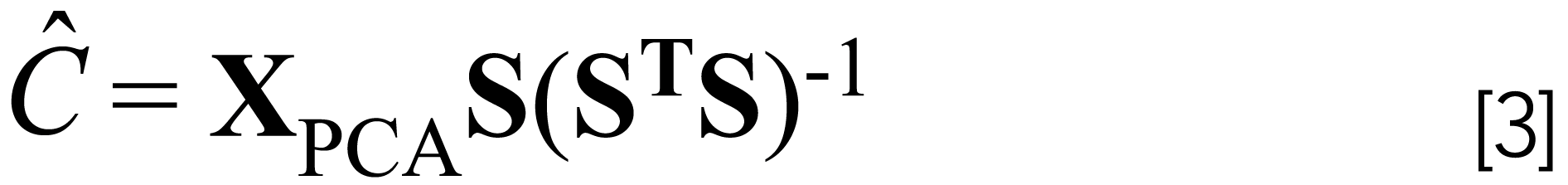
Our previous experience with ALS has shown that initial estimates of the concentration (score) matrix are crucial to rotate C and S^T toward a feasible solution. Although there is no one technique that is successful with all datasets, our experience is that the varimax extended rotation (VER) provides a good initial estimate of C in ALS. The goal of VER (12,13) is to find regions in a spectral image that contain only a single component, and use these regions to obtain the spectral profile of each component. This is accomplished through a three-step procedure. First, the spectral data are preprocessed. Preprocessing involves several steps. Each IR spectrum is normalized to 100. Normalization to constant row sum ensures that each spectrum is weighted equally in the analysis, but the dimensionality of the data is reduced by one. Next, each wavelength is range scaled. Range scaling allows for the extremum points in the data to be identified, which is important since these points may be pure components or nearly pure components. Range scaling opens up the data, recovering the dimension lost in the previous step. Finally, each row vector is normalized to unit length. Normalization of the data to unit length accounts for changes in the optical path length, ensuring that any observed variation in the data is due only to changes in the composition of the constituents. Normalization to unit length also allows each spectrum to serve as a potential basis vector for a new coordinate system. Normalizing each row vector to unit length also reduces the dimensionality of the data by one. Using this preprocessing scheme, the data are closed, opened, and closed again.

The second step of VER involves PCA, which reduces the dimensionality of the data while simultaneously retaining the information present in the original data. In the third and final step, a new coordinate system is developed for the data using a varimax rotation (14) followed by an extended rotation (15,16) to assist in the identification of the regions containing only a single component while simultaneously rotating the score and loading matrices toward a feasible solution using these regions. The transformed score matrix from VER serves as an initial estimate of C in ALS.

Modified Alternating Least Squares

Although ALS is reasonably fast and produces reliable results for large data sets, the method suffers from drawbacks that can degrade performance and reliability for many types of imaging data sets. Processing speeds for ALS are often slow, due to convergence problems and sensitivity to highly correlated data. When constraints such as non-negativity or unimodality are applied, ALS may be slow to converge even though each individual iteration is fast. Modified ALS (MALS) (17) is a solution to the constrained non-negative least squares optimization problem for infrared and Raman imaging. MALS is appealing, as it is fast, accurate, and robust.

MALS is a modification of ALS (see equations 4 and 5). This modification involves the addition of two terms to equations 2 and 3, where S₀ and C₀ are the previous estimates of S and C and w_s and w_c are weights that are determined dynamically. The first term in equation 4 (w_sI_p) and the second term in equation 5 (w_cI_p) transform ALS into a ridge regression algorithm that allows the least squares solution to be robust towards collinear data. The second term in equation 4 (w_sS₀^T) and the first term in equation 5 (w_cC₀) compensate for the bias that occurs when using ridge regression. As the least squares solution moves toward convergence, the bias decreases until it is zero or near zero at the time of convergence. The values of the weights (w_s and w_c) during each iteration are adjusted such that they are proportional to the magnitude of the difference between the updated C matrix and the previous iteration of C or the updated S matrix and the previous iteration of S, but are scaled to the size of the factor space preventing the weights from becoming too small or too large.

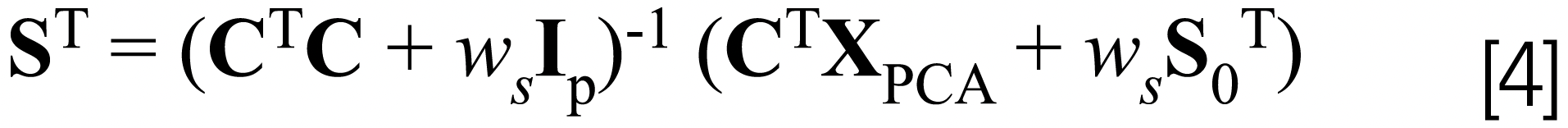
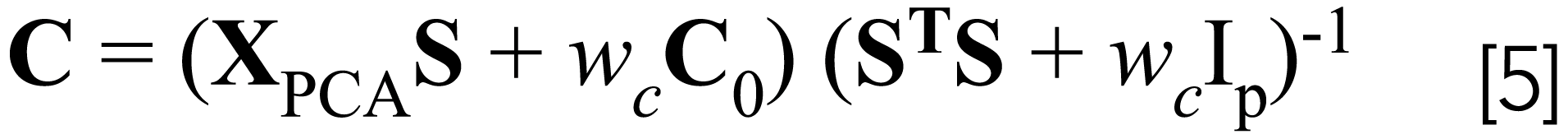
Using Raman imaging data of water in oil emulsions, the efficacy and efficiency of MALS to resolve spectral images was demonstrated (1). The data were collected by mapping a 31 × 35 μm area in the X and Y dimensions with 6 cm^-1 resolution, using a Kaiser HoloScope 785 nm Raman system with an optical fiber coupled to a Zeiss Microscope. The microscope was equipped with a 100X/0.80 objective. The data set consisted of 1085 spectra of 1201 wavelengths per spectrum for a total of 1.3 million data points. The CCD exposure time on the Raman system was set to 18 sec at each pixel location. The oil-in-water emulsion consisted of an alkyl ester, alkyl ethoxylate, alkyl parabens, glycerol, and water. It was determined that four principal components were necessary to describe the data matrix for the emulsion. Recovered spectra of these four components from MALS were compared to spectra of the original components comprising the emulsion, and good matches were obtained. A comparison of the two sets of estimates (MALS versus ALS) showed that MALS performed significantly better at estimating the component spectra than ALS.

In another study (2), infrared spectra from all layers of an intact multilayered automotive paint chip were collected in a single analysis by scanning across each layer of a cross-sectioned automotive paint chip using an iN-10 MX Fourier transform infrared (FT-IR) imaging microscope (Thermo-Nicolet). Applying MALS to the IR spectral data, the IR spectrum of each layer of an original equipment manufacturer (OEM) paint chip was successfully extracted from a line map of the spectral image. In this study, small paint chips (1 mm or less) were cross-sectioned using an ultramicrotome, which does not require epoxy or other embedding media for the paint chip, thereby simplifying the analysis. However, extracting the IR spectra for each layer of an OEM paint chip by ALS was problematic for these thin peels. MALS was able to recover the IR spectrum of each layer. By using a new sample preparation technique and the appropriate multivariate curve resolution method, high quality IR spectra of the layers of modern automotive paints were obtained from paint fragments that are smaller than what is practical to analyze by conventional FT-IR spectroscopy.

Conclusions

MALS is superior to ALS for the analysis of infrared and Raman image spectral data because of the stability of ridge regression methods, and the speed advantage due to the kernel nature of the MALS algorithm that reduces the computational overhead of typical ridge-regression (and ALS) methods. MALS can resolve the basis vectors characteristic of the components comprising the sample even when the data is low signal-to-noise and nearly collinear. For image data with these attributes, MALS in most cases can produce a satisfactory convergent solution, whereas ALS often fails. The performance of MALS for spectroscopic imaging problems, like other ALS methods, is also influenced by the spatial resolution between sample components, since low spatial resolution produces a greater mixing of components within the image.

Acknowledgments

The authors acknowledge the financial support of Phillips 66 and the National Science Foundation (CHE-2003867). Both BKL and TMH wish to acknowledge the pioneering efforts of Edmund Malinowski in the area of self-modeling curve resolution methods.

References

(1) Wang, J.- H.; Hopke, P. K.; Hancewicz, T. M.; Zhang, S. L. Application of Modified Alternating Least Squares Regression to Spectroscopic Image Analysis. Anal. Chim. Acta 2003, 476, 93–109. DOI: 10.1016/S0003-2670(02)01369-7

(2) Zhong, H.; Donkor, E.; Whitworth, L.; et al. Application of Ultramicrotomy and Infrared Imaging to the Forensic Examination of Automotive Paint. J. Chemom. 2023, e3509. DOI: 10.1002/cem.3509

(3) de Juan, A.; Tauler, R. Multivariate Curve Resolution: 50 Years Addressing the Mixture Analysis Problem – A Review. Anal. Chim. Acta 2021, 1145, 59–78. DOI: 10.1016/j.aca.2020.10.051

(4) Ruckebusch, C.; Blanchet, L. Multivariate Curve Resolution: A Review of Advanced and Tailored Applications and Challenges. Anal. Chim. Acta 2013, 765, 28–36. DOI: 10.1016/j.aca.2012.12.028

(5) de Juan, A.; Casassas, E.; Tauler, R. "Soft Modeling of Analytical Data," in Encyclopedia of Analytical Chemistry: Instrumentation and Applications; Wiley, 2000, Vol. 11. DOI: 10.1002/9780470027318.a5208

(6) Tauler, R.; de Juan, A. “Multivariate Curve Resolution,” in Practical Guide to Chemometrics, 2nd Edition; Gemperline, P., Ed.; CRC Press/Taylor & Francis, 2006.

(7) Geladi, P.; Grahn, H. Multivariate Image Analysis; John Wiley & Sons: NY, 1996.

(8) Smilde, A.; Bro, R.; Geladi, P. Multi-way Analysis; John Wiley & Sons, 2004.

(9) Tauler, R. Multivariate Curve Resolution Applied to Second Order Data. Chemom. Intel. Lab. Syst. 1995, 30 (1), 133–146. DOI: 10.1016/0169-7439(95)00047-X

(10) de Juan, A.; Vander Heyden, Y.; Tauler, R.; Massart, D. L. Assessment of New Constraints Applied to the Alternating Least Squares Method. Anal. Chim. Acta 1997, 346, 307–318. DOI: 10.1016/S0003-2670(97)90069-6

(11) Jackson, J. E. A User’s Guide to Principal Component Analysis; John Wiley & Sons, 1991.

(12) Lavine, B. K.; Ritter, J. P.; Voigtman, E. Multivariate Curve Resolution in Liquid Chromatography-Resolving Two-Way Multi-Component Data Using a Varimax Extended Rotation. Microchem. J. 2002, 72, 163–178. DOI: 10.1016/S0026265X(02)00029-2

(13) Lavine, B. K.; Davidson, C. E.; Ritter, J. P.; Westover, D.; Hancewicz, T. Varimax Extended Rotation Applied to Multivariate Spectroscopic Image Analysis. Microchem. J. 2004, 76, 173–180. DOI: 10.1016/S0026-265X(03)00159-0

(14) Harman, H. H. Modern Factor Analysis, 3rd Ed. University of Chicago Press, 1976.

(15) Miesch, A. T. Q-Mode Factor Analysis of Geological and Petrological Data Matrices with Constant Row Sums. United States Government Printing Office: Washington DC, 1976, pp. G1–G47.

(16) Miesch, A. T.; Klovan, J. E. Extended Cabfac and Qmodel Computer Programs for Q-Mode Factor Analysis of Compositional Data. Comput. Geosci. 1976, 1 (3), 161–178. DOI: 10.1016/0098-3004(76)90004-2

(17) Hancewicz, T.; Wang, J. H. Discriminant Image Resolution: A Novel Multivariate Image Analysis Method Utilizing a Spatial Classification Constraint in Addition to Bilinear Nonnegativity. Chemomet. Intellig. Lab. Syst. 2005, 77, 18–31. DOI: 10.1016/j.chemolab.2004.07.013

Barry K. Lavine is with the Department of Chemistry at Oklahoma State University, in Stillwater, Oklahoma. Thomas M. Hancewicz is with Thomas Mark Hancewicz Consulting in Whitehall, Pennsylvania. Direct correspondence to: bklab@chem.okstate.edu