The Inductively Coupled Plasma Source

Heumann and colleagues (3) carefully studied the accuracy and precision attainable for isotope ratio measurements using ICP-MS. This work supported the emergence of plasma sources as commercially available alternatives to thermal ionization and glow discharge sources. This work described the measurement metrics rather than techniques used to extend the limits of detection to lower and lower levels, an interest driven by the promise that isotope-ratio measurements could be extended to a much larger sample population, and that interest in isotope dilution MS also supported the need for a greater number of measurements of isotope ratios. They discussed the source factors (as contrasted with system factors) affecting mass discrimination and summarized possible correction methods for the mass discrimination effects encountered. Since the time of this study, many other correction factors have been proposed, as covered briefly at the end of this column. In attention to precision and accuracy for measurements in ICP-MS, the work of Heumann and colleagues and those who followed reflects the earliest days of the development of the EI source. Organic analysis using the EI source does not typically require the same degree of rigor in characterization of the source for a mass discrimination effect, although EI sources used in extraterrestrial applications are exceedingly well characterized. The two factors that we explore here are the space charge effect and the nozzle expansion effect.

Kenneth L. Busch

The end result of space charge in an ICP source, as it is in any other source used for MS, is mass discrimination. The basics of space charge have been discussed previously in this column (4). The skimmer cone samples a subset of this ion population, and the sampled ions then have to pass through the ion optics into the mass analyzer of the instrument. Space charge (the mutual repulsive force between ions of like charge) distorts the extraction and focusing effects of the ion optics, just as in any other ionization source used for MS.

An early demonstration of this phenomenon followed the effect exerted by the presence of Pb⁺ ions on the signal measured for Li⁺ ions and highlighted the role of mass in determining the magnitude of the space-charge effect (5). The path of the heavy ions is less distorted by space charge than the light ions, so there is a systematic discrimination against the lighter ions in a multicomponent ion beam. The extent of the mass discrimination effect will depend upon both the distribution of components in the ion beam (and is therefore a matrix effect), and on the total ion current drawn from the ICP source.

A mass discrimination factor can be determined (for a particular system) using repetitive analyses of a standard multicomponent mixture. Heumann and colleagues (3) reported that the mass discrimination factor per mass unit is about 10% for mass values less than 10 Da, between 1% and 5% for mass values of about 20–150, and less than 1% only for the higher mass values. The practical consequence of the mass discrimination effect in the working range for most elemental analysis is a correction factor (called the mass discrimination factor) based upon space charge alone of between 1% and 5%. The need is clear for careful and repetitive analysis of both standards and samples, under constant instrumental conditions, to make accurate isotope-ratio measurements. A mass discrimination factor determined on one instrument cannot be translated to a second instrument, nor to different source operating conditions on the same instrument.

As a brief aside, the influence of operating conditions is illustrated in Figure 1, which shows the different isotope ratios measured for a standard copper sample as the potential on a single lens in the ion optics is changed. To be rigorous, the points in the graph should each have associated error bars so that the magnitude of the change can be assessed, and the change itself is relevant to measurements performed only at one value of total ion current extracted from the source. In this particular instance, an increasing potential applied to the lens slows the ions and magnifies the apparent effect of the space charge. Thus, the effect is consistent with expectations based upon our understanding of space charge; the magnitude of the effect and its subsequent correction is paramount in accurate isotope-ratio measurements.

Figure 1

The space-charge effect can be examined and predicted through modeling. As ICP-MS sources were characterized in the late 1990s for mass discrimination effects, it was hypothesized that such effects would be minimized in sector-based instruments compared with quadrupole-based instruments. The postulate was based upon the assumption that the higher accelerating voltage of the sector would penetrate the source and reduce the magnitude of the space charge effect, drawing ions out into the mass analyzer at higher velocities.

The same hypothesis was made in EI sources; ion modeling studies for the EI source show, however, that the actual penetration of the extraction potential into the source optics was minimal. In studies of the ICP source, measurements (based upon a comparison of measured with standard reference isotope ratios) show that the mass discrimination factors with a sector instrument are still in the range of a few percent. They are reduced only slightly for higher mass ions (compared with a quadrupole-based instrument), and they are almost identical for the lower-mass ions. In addition, this series of measurements suggested that the primary region in which space charge operates to create the mass discrimination effect is the volume between the plasma and the skimmer cone, rather than in subsequent sections of the source interface.

ICP sources differ from EI sources in that observed mass discrimination effects are related to another element of source operation, one that is not specifically accommodated in ion modeling programs. Heumann and colleagues (3) investigated changes in the mass discrimination factors that occurred when the flow rates of the aerosol gas and the plasma gas were changed. The flows of these gases affect the stability of the plasma and the dynamic behavior of the ions formed in the plasma. The dynamic space charge effect leads to changes in the observed mass discrimination effect. In the particular instrument used as the platform for the studies, changes in the flow rate of the nebulizer gas exhibited a much stronger effect on the subsequent mass discrimination factors than changes in the flow of the plasma gas. Furthermore, the magnitude of this effect (over the range studied) was of the same scale as changes in the potentials of lenses within the ion optical stack.

An implicit assumption in our previous discussion of the detailed design of the EI source is that the flux of sample into the source was relatively constant, as was the pumping capacity that removed molecules from the source and source region. A more detailed analysis that follows changes in the efficiency of an EI ion source as the gas flow changes is not usually pursued. In gas chromatography (GC)–MS, while it might seem that the flow of gas into the source changes significantly as a peak of a sample moves into the source, this is not the case. The flow of the carrier gas (often helium) remains relatively constant. The flow of the sample itself is but a small fraction of the total gas flow, so the elution of a peak results in no substantive change in the overall flow rate.

Clearly, as described earlier, the gas dynamics of a source such as the ICP are different. A shift in the flow rates of those gases leads to a shift in the actual physical dimensions of the plasma, a change in its ion transport properties, and a shift in the effects that might be observed due to space charge. There is, however, another concomitant effect that should come as no surprise. In the work of Heumann and colleagues (3), this is called the nozzle separation effect. The origin of this effect is in the elementary gas laws that govern the rates of diffusion and effusion for gases of different masses. Should this sound intimidating, pull your elementary chemistry textbook off its shelf and look up Graham's Law. This principle forms the basis for some of the earliest (and now recurring) methods of separation of isotopes. Those who remember the development of earlier interfaces for packed columns to mass spectrometers will recall the basic principles in the design of the jet separator.

The discrimination effect that modifies the transport of lighter and heavier species through a region of varying pressure is independent of whether the species carries a charge or not. Whereas the space charge effect underlies the differential movement of ions and is dependent upon the total ion current drawn through the interface, the nozzle separation effect operates on both molecules and ions and does not exhibit a dependence on the total ion current. The region between the plasma torch and the skimmer cone in an ICP source is where the nozzle separation effect plays out. Contributions to the observed mass discrimination factor based upon the nozzle separation effect are in the same direction as the effects due to space charge. Breaking out the separate contributions based upon a system that ultimately detects only the ions has been difficult, but the contributions to the overall discrimination are expected to be similar, based upon the connection of the changes in nebulizer gas flow (described earlier) and its observed effects. The detailed schematic of an ICP-MS source shown in Figure 2 includes the nozzle separation effect in its concept. Graphically (and conveniently), the light ions (L⁺ ) are physically smaller, and the heavy ions (H⁺ ) are physically larger. The figure is not drawn to scale, of course, and the excellent exercise to calculate just how far off scale it actually is would benefit the reader.

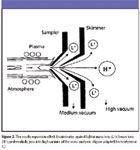
Figure 2

We have not covered here other factors that affect the accuracy and precision of measurements carried out with ICP-MS. These include effects due to the statistics of ion counting, the stability of the ion current drawn from the plasma source, the occurrence of isobaric interferences (ions of the same mass but representing different species), cross-talk in abundance sensitivity (the presence of an abundant isotope of mass adjacent to an isotope of much lower abundance, with cross-talk caused by overlap in peak profile), mass-analyzer discrimination, and detector discrimination.

Corrections of some of these factors require special instruments such as those equipped with multiple ion collectors. But many of these factors, together with the space-charge effects and nozzle separation effects discussed here, can be accounted for with several kinds of mathematical corrections to measurements. Usually these corrections are based upon a concurrent analysis of standard reference samples, or a sample of known isotopic composition. The corrections are, of course, important in the various procedures used in isotope dilution MS, but also for the various elements for which natural variations in isotopic abundances are known to be significant. These include the lighter elements such as lithium and boron and elements such as carbon, nitrogen, and oxygen for which biological processes contribute to observed variations. Special calibration procedures are used in these instances for which the variations are measured at very low levels.

For elements in which no naturally expected isotopic variation is expected, calibration via a mass discrimination factor can take several forms. Instrument performance can be calibrated through the use of a naturally occurring sample for which the isotopic composition is known. In cases in which some variation might be expected, an element of known isotopic composition of similar mass can be used to calibrate instrument performance. Most rigorously, the instrument performance can be established via repetitive measurement of a wide variety of certified reference standards. This last method is the most time consuming, but it generally yields results of the highest accuracy and precision.

A comparison of mathematical correction techniques has been completed by Mason and colleagues (6). Correction also is needed for multiple collector instruments (7), in which the source mass discrimination might play a more prominent role.

Finally, we have focused here on the ICP source itself, and explored its characteristics that can lead to mass discrimination effects. The performance characteristics of the detector also contribute to an uncertainty in isotope ratio measurements. Appelblad and colleagues (8) explored the sources of uncertainty derived from the use of a single detector design in ICP-MS. The effects of flicker noise and white noise are poised against the effects of mass discrimination and dead-time corrections. Under most experimental conditions, it is the latter that makes the predominant contribution to uncertainty, which underscores the importance of understanding the origin of the mass discrimination effect in the ICP source itself.

Kenneth L. Busch is sometimes confused by the cleavages and rearrangements seen in mass spectra or organic compounds, and by the devious paths through which ions sometimes choose to dissociate. Along with Tom Lehrer, then, he takes solace in the harmony of the simple elements and their mass spectra. This column represents the views of the author and not the National Science Foundation. The author can be reached at WyvernAssoc@yahoo.com

References

(1) R.C. Willoughby, "How Do We Eliminate Ion Losses at AP?" available at the LCMS homepage, www.lcms.com.

(2) R. Thomas, Spectroscopy16(6), 26 (2001).

(3) K.G. Heumann, S.M. Gallus, G. Rädlinger, and J. Vogl, J. Anal. Atom. Spectrom.13, 1001 (1998).

(4) K.L. Busch, Spectroscopy19(6), 35 (2004).

(5) L.A. Allen, J.J. Leach, and R.S. Houk, Anal. Chem.69, 2384 (1997).

(6) T.F.D. Mason, D.J. Weiss, M. Horstwood, R.R. Parrish, S.S. Russell, E. Mullane, and B.J. Coles, J. Anal. Atom. Spectrom.19, 218 (2004).

(7) F. Wombacher and M. Rehkamper, J. Anal. Atom. Spectrom.18, 1371 (2003).

(8) P.K. Appelblad, I. Rodushkin, and D.C. Baxter, Anal. Chem. 73, 2911 (2001).