The Role of Naturally Occurring Stable Isotopes in Mass Spectrometry, Part III: Small Gas Molecule Calculations

In the third installment of this tutorial, the authors explain the determination of the isotopic composition of a sample from a mass spectrometric measurement, and the methods of calculation as well as the units used. This tutorial outlines the practices in common usage so that researchers new to this field can obtain a good understanding of the fundamentals involved.

The reporting of isotopic compositions from mass spectrometric (MS) measurements is not a straightforward matter because in most cases, some degree of correction is necessary to extract the true isotopic composition from the measured ion currents. Also, there is no consensus on the units in which to make the report (1). As the measurement technology and its role in the application progressed, both the methods of correction and the units have developed independently for each isotopic species under investigation. Originally, isotope practice was developed to determine small changes in natural abundance, and the notations and conventions adopted are considered by some to be unsuitable for modern high-throughput, high-enrichment work, as is practiced in tracer techniques (2).

The rationalization of stable isotopic composition reporting by the adoption of the International System of Units (SI) has been considered recently (3). In fact, the "natural" way of reporting isotopic composition is to use fractional abundance, F, defined as the quantity of a particular isotope divided by the total quantity of that element in the sample. Fractional abundance is therefore a dimensionless quantity, closely analogous to mole fraction. Unfortunately, in cases of polyisotopic species, it is often not possible to measure all of the isotopes present, and recourse is made to normalizing the quantity of the particular isotope to that of the major (most abundant) isotope present. On this basis, the isotopic abundances, R, defined in terms of the ratio to the major isotope, are related to fractional abundance via

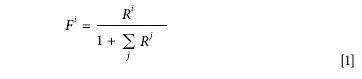
where the subscript i specifies the particular isotopic species, and the summation runs over all the isotopes present.

Many researchers prefer to express abundance as the deviation from that observed in some standard material, and this gives rise to the concept of excess abundance ΔRⁱ_samp = Rⁱ_samp – Rⁱ_std. This scheme is favored by scientists working with nitrogen isotopes, who often quote abundance in terms of atom percent excess.

Scientists working with other light isotopes such as hydrogen, carbon, and oxygen, in the geochemical field, took this one step further and adopted a scale known as the delta value, defined in the next section; this is currently the most adopted way of reporting isotope determinations using commercial instrumentation.

The Delta Value

A mass spectrometer can never provide an absolute measurement of ion beam intensity. For a given partial pressure of gas in the inlet, the signal recorded at the detector is influenced by the ionization efficiency of the source for that particular species, the transmission of the ions through the mass analyzer, and the gain of the various amplifiers used in the ion detection (active devices such as the electron multiplier as well as the electrometers used for final stage amplification). Not only are all of these factors governed by the actual experimental conditions at the time of measurement (such as ambient temperature, ion source cleanliness, and state of instrument tuning), but they all are also subject to drift throughout the working day, and often within the timescale of the experiment being performed. Isotope ratio mass spectrometers are designed to minimize these effects. For example, they usually are operated in flat-topped peak mode (4,5), which minimizes the effect of mass drift. Secondly, they use Faraday buckets rather than electron multipliers as detectors because of the greater stability of the former. Finally, arrangements usually are made for simultaneous measurement of all of the ion beams required and the results reported as the ratios of the ion currents relative to the major beam. Even with these precautions, the ratios obtained are not absolute (principally because of uncertainty in the values of the feedback resistors of the electrometer amplifiers), and still are subject to drift because of sensitivity to ambient temperatures.

The effects of drift can be eliminated by the inclusion of a standard sample in the experiment. In the case of continuous flow instruments, this is achieved by admitting a pulse (or pulses) of reference (cylinder) gas to the instrument as part of the measurement sequence. In dual inlet systems, where the sample and reference gases are each held in bellows connected to a microvalve, a series of alternate measurements of the ratios obtained from the two gases are made. In either case, the reported measurement of isotope ratios is a comparison between the measurements made on the sample and the reference materials. The conventional way of expressing enrichment is on the delta scale, defined as, intercomparison, working or transfer standard, and internal or reference standard (6).

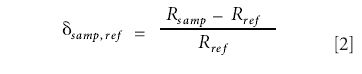
In this equation δ_samp,ref indicates the delta value of the sample with respect to the reference, and R_samp and R_ref are the ratios of the ion currents measured for the sample and reference gases, respectively. Delta values often are multiplied by 1000, and therefore expressed as "parts per mill" (or just "per mill," in accordance with the English edition of the International Standard ISO 31-0, Quantities and Units – Part 0: General Principals, sub-clause 2.3.3), symbol ‰†. As an example of how the delta value is obtained from the raw ion currents, we take the output from a dual inlet machine. For simplicity, we assume that it is measuring m/z 44 and 45. The measurement sequence comprises four determinations of the reference gas alternated with four measurements of the sample gas, giving the results shown in Table I.

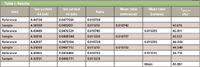
Table I: Results

Note how the delta value is calculated for each sample measurement by comparison with the average ratios of the reference measurements made immediately before and immediately after it, with a similar strategy being applied to each reference measurement.

In passing, it is worth discussing to what extent the strategy of using a reference gas can eliminate drift during the course of a series of measurements. For correcting short- to medium-term fluctuations due to such factors as ion source conditioning, it is highly successful. However, not all sources of drift can be corrected in this way, and care must be taken that the process itself does not introduce errors. For example, in dual-inlet systems the reference gas is stored at subatmospheric pressure in a set of bellows. Each time this gas is admitted to the mass spectrometer, there is likely to be some fractionation due to the pumping characteristics of the vacuum system. In other words, as the experimental run progresses, the isotopic composition of the reference gas is likely to change gradually, becoming more enriched in the heavier species. Although instruments are designed to minimize this problem, it can be noticeable in the most precise work. The introduction of a drift of this nature is much less likely in continuous flow systems, where the reference gas is stored and injected at much higher pressures.

Properties of Delta Values

The mathematical manipulation of delta values must be undertaken with care. For example, consider the delta value of some material A, expressed with respect to another material B

However, the reciprocal term is

Combining Delta Values

The isotopic composition of any gas can be expressed relative to that of another gas by means of a delta value. For example, suppose we also have a standard gas and we conduct an experiment in which our reference gas is used as the sample and measured with respect to the standard. We would obtain the following delta value:

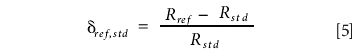
Simple rearrangement allows us to express R_ref in terms of δ_ref,std and R_std, thus

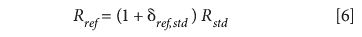
which can be substituted in equation 2 to obtain

Therefore,

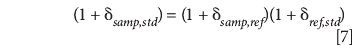
As an example, suppose we know that the reference gas has a delta value of –17.9‰ with respect to an international standard. We can express the enrichment in our sample by

or 25.2‰ with respect to the standard.

International Isotope Standards

The generally accepted agency for the definition and supply of stable isotope standards for light elements is the International Atomic Energy Establishment (IAEA)]. The IAEA distinguishes six types of reference material that it denotes primary reference, calibration, reference, intercomparison, working or transfer standard, and internal or reference standard (6), although some of these terms are used in different contexts by other authors. They can be summarized as follows:

Primary reference material — a material that is generally agreed to be a standard against which isotopic abundances of other materials are expressed. It is used to define a scale for reporting variations of stable isotopic composition.

Calibration material — a material that has been carefully calibrated against the primary reference material and for which the calibration values have been internationally agreed. It is used as a proxy for the primary reference if the primary reference is not available.

Reference material — a material that has been calibrated against the primary reference and that is believed to be sufficiently homogenous for the isotopic composition to be stated with well-defined uncertainties.

Intercomparison material — a material of proven homogeneity that allows interlaboratory comparisons of measurements to be made.

Working standard — a gas used as the reference gas in the MS measurement. This is not a standard in the usual sense, as it merely acts as a means of indirect comparison between prepared samples and reference materials.

Internal standard — a material routinely run as a sample as quality controls in the MS analysis.

For hydrogen and oxygen analysis, it has been accepted for more than 50 years that ocean water should be used as the primary reference material, as this represents the largest available reservoir on earth. Unfortunately, ocean water itself is not sufficiently homogenous, and so a hypothetical mixture of waters taken from various sampling sites was proposed and given the title Standard Mean Ocean Water (SMOW) (7). For carbon analysis, CO₂ generated from a geological formation in the U.S. (PeeDee Belemnite, PDB) was adopted (8). The nitrogen standard is taken as atmospheric N₂, while for sulfur work, a material from a meteorite, Cañon Diablo Troilite (CDT), was adopted.

Because SMOW is a purely hypothetical material and the stocks of PDB and CDT are exhausted, these primary references are unavailable and have been replaced by synthetically prepared analogues named VSMOW, VPDB, and VCDT, respectively (Table II). In each case, the V stands for Vienna, where the headquarters of the IAEA is situated. To clarify the relationships between these primary references and the other types of standards defined earlier, the particular case of the water standards used for hydrogen and oxygen work will be examined.

Table II: Primary references for selected light elements

The primary reference VSMOW was prepared to have as close an isotopic composition to the purely conceptual SMOW as possible. At the same time as VSMOW was prepared, two reference materials also were obtained. The first, derived by melting Antarctic ice, was named SLAP, for Standard Light Antarctic Precipitation (originally this water was known as SNOW, but this was changed in order to avoid confusion with SMOW). It is substantially depleted in heavy isotopes of both hydrogen and oxygen with respect to VSMOW. The second reference material, again obtained by melting ice, this time from Greenland, has isotopic composition intermediate between VSMOW and SLAP, and is called GISP (Greenland Ice Sheet Precipitation). In addition, the opportunity was taken to recalibrate two existing U.S. water standards, NBS-1 and NBS-1A, onto the VSMOW scale. This gave a grand total of five reference materials, as indicated in Table III. Because the isotopic composition of these waters is internationally agreed, they now can be regarded as calibration materials if so required.

Table III: Reference materials for 2H and 18O analysis

In addition to supplying small samples of these calibration materials, the IAEA offers the reference materials IAEA-302A & B (ä³ = 508.4‰ and 996‰) and IAEA-304A & B (ä¹⁸ = 251.7‰ and 502.5‰), respectively. Some laboratories choose to prepare their own reference materials and to have them calibrated against V_SMOW independently. For example, in Cambridge, we currently use local tap water (–49.0‰) and a series of gravimetrically prepared standards in the range –49 to 874‰. Our reference materials are incorporated into every analytical run and are used not only for two-point calibration of the mass spectrometer (see SMOW/SLAP correction below), but also to check linearity, thereby adopting the roles of internal standards.

Is the delta scale the best choice?

When these measurements are made, each sample or standard is compared directly with a reference gas, as described earlier. This working standard is used solely for the purpose of allowing samples to be compared with each other, and therefore can be of arbitrary source. We use standard cylinder (tank) hydrogen for this purpose. The isotopic composition of the working standard is unimportant in this case because both reference materials and samples are incorporated in the same run; therefore, it is assigned the value of 0‰ on the reference scale, and all measurements are made with respect to this. Once all these results have been obtained, they are converted to the VSMOW scale using the data from the reference materials.

Calculations Peculiar to Specific Isotopes and Compounds

Hydrogen, H₂

The H₃⁺ correction

There is a complication peculiar to gaseous hydrogen when measuring isotope ratios by mass spectrometry. The isotopologues of interest are ¹H₂⁺ (m/z 2) and ¹H²H⁺ (m/z 3). There is an ion-molecular reaction, however, which occurs in the ion source, ¹H₂⁺ + ¹H₂ → ¹H₃⁺ + ¹H^·, which gives rise to a second species at m/z 3. Consideration of the kinetics shows that if the ion current at the major collector is denoted I_2, then the ion current at the minor collector will

where R is the required ratio for calculating isotopic abundance and K is an experimentally determined constant, known as the H₃⁺ correction factor. Dividing equation 9 by the major ion beam intensity gives

where R* is the actual measured ratio of ion currents.

For dual-inlet instruments, the H₃⁺ correction factor is relatively stable and measured very easily by admitting reference gas at a series of different pressures and performing linear regression of the measured ion current ratios (R*) against the major beam ion currents (I₂). Typically, K is found to have a value of 5 ppm/nA, and therefore with an operating major ion beam of 5 nA, the actual ratio measured is some 25 ppm in excess of the true ²H¹H/¹H₂ ratio.

In contrast, correction for H₃⁺ formation in a continuous flow experiment is much more complex. Not only is the isotope ratio measurement made over a large range of partial pressures of hydrogen so that the contribution to the minor beam from H₃⁺ is initially zero, rises to a maximum, and drops back down to zero, but helium usually is used as a carrier gas, which in itself can alter the magnitude and mechanism of the H₃⁺ formation. Two basic approaches to this problem have been proposed, deemed pointwise and piecewise methods (9). In the pointwise strategy, each measured value of the minor beam is correct based upon the corresponding value of the major beam, while in the peakwise approach, the correction is applied based upon the area under the major peak (that is, the overall intensity of the signal). A rigorous investigation has shown that despite the appeal of the pointwise method, limitations in current spectrometer design make the peakwise method more suitable.

The SMOW/SLAP correction

As is common with many analytical techniques, the instrumental response to hydrogen isotope ratios is linear but does not necessarily pass through the origin. The usual way to overcome this is to use a two-point calibration curve, and this is the basis of the SMOW/SLAP correction, often informally referred to as the "stretch factor."

Suppose two standard samples (denoted std1 and std2) are measured along with a sample (samp) with respect to an arbitrary reference gas. If the delta scale is linear, then

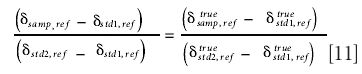
Rearrangement of this equation gives the generalized "stretch" equation

Where

is the "stretch factor."

Consideration of equation 11 will indicate that the value of either side in the equation is independent of the reference gas used. Therefore, without loss of generality, we can use delta values with respect to std1 on the right hand side to obtain (remembering that ä_std1,_std1 = 0 by definition).

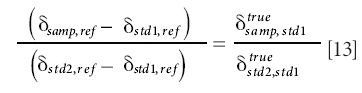
In the particular case when std1 is SMOW and std2 is SLAP, this re-arranges to

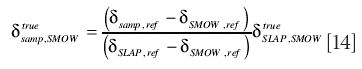
as indicated in the IDECG working group report (10).

However, in the general case, SMOW and SLAP will not be available in the laboratory to be used in this way, and the two standards will be secondary ones traceable back to the primary source. In this case, it is prudent to express both measured and true isotopic composition with respect to std1, in which case the generalized stretch equation becomes

Example calculation

Two reference materials are used to calibrate the mass spectrometer. The first, std1, has been calibrated at

Calculation gives

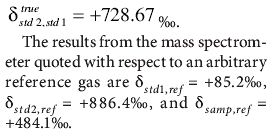
The first step is to express all enrichments as delta values with respect to std1 using the formula for manipulating and combining delta values (equations 4 and 7):

or 367.6‰

Similarly, δ_std2,_std1 = 738.2‰, from which we calculate

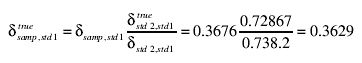
or 362.9‰.

Finally, we can re-express this with respect to VSMOW to obtain

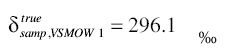
Nitrogen, N₂

Nitrogen gas has three isotopologues:

¹⁴N¹⁴N, m/z 28

¹⁵N¹⁴N, m/z 29

¹⁵N¹⁵N, m/z 30

In general, a sample comprising Q²⁸ moles of ¹⁴N¹⁴N, Q²⁹ moles of ¹⁵N¹⁴N, and Q³⁰ moles of ¹⁵N¹⁵N will contain 2Q²⁸ + Q²⁹ moles of ¹⁴N and Q²⁸ + 2Q³⁰ moles of ¹⁵N, and so the fractional abundance of ¹⁵N will be

This formula is exact and applies even if the molecular species are not in isotopic equilibrium. However, if the enrichment is low, there often can be a significant contribution to m/z 30 due to trace quantities of nitric oxide (NO). In this case, isotopic equilibrium must be assumed, whence the usual calculations (4,5) can be applied:

F²⁸ = (F¹⁴)²

F²⁹ = 2F¹⁴ F¹⁵

F³⁰ = (F¹⁵)²

Therefore,

in which case

Carbon Dioxide, CO₂

The CRAIG Correction

Carbon dioxide gas is used as a convenient vehicle for measuring ¹³C/¹²C and ¹⁸O/¹⁶O isotopic abundances. As a rough approximation, the ratio of m/z 45 to m/z 44 corresponds to the carbon contribution, and that of m/z 46 to m/z 44 to oxygen. Unfortunately, the presence of a second minor isotope of oxygen, ¹⁷O, is a confounding factor, with the ion beams comprising the following isotopic species:

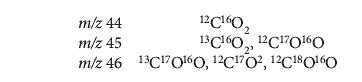
There are essentially three unknowns to be found (¹³C/¹²C, ¹⁷O/¹⁶O, and ¹⁸O/¹⁶O), but only two independent variables to measure (m/z 45/44 and m/z 46/44). From the elemental fractional abundances for the general gas denoted A (see B&V1):

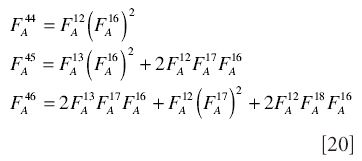
and hence the ratios are

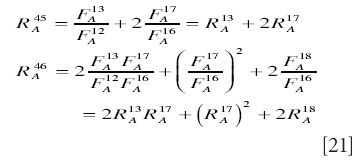
If we work in terms of delta values measured with respect to some standard, we first note that equations precisely analogous to those presented earlier apply to the standard material, that is,

Secondly, by the definition of the delta value, the general ratio is

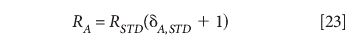
and so

Rationalizing within these simultaneous equations gives

Craig's approximation (8) amounts to neglecting square and higher powers of the delta values (based upon the assumption that the sample and standard have similar isotopic compositions), and also taking

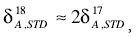
the root of the assumption being the square-root law of fractionation. Therefore, on substitution and re-arrangement:

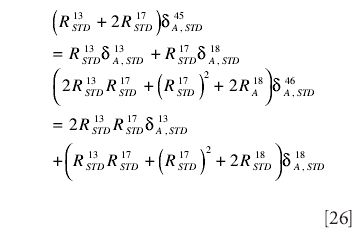
The standard is usually taken to be PDB, for which the elemental composition is well established

From these the molecular ratios,

Using these values in the expressions for

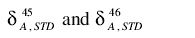
gives

Finally, these can be inverted to give the equations of the Craig correction:

Example calculation

As an example of the correct usage of the Craig correction, as well as pointing out a commonly made error, we will examine a measurement made on a sample using a reference gas calibrated against PDB. We suppose that the reference gas has

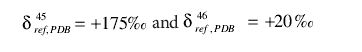
and the measurements made are

The correct procedure is to first express the delta values for the sample with respect to PDB:

The elemental compositions are then obtained by applying the Craig correction:

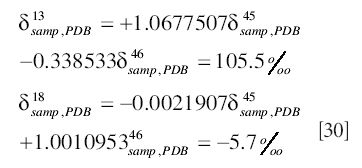
A common mistake is to apply the equations of the Craig correction before expressing the delta values with respect to PDB; this error has been observed even in software supplied by one of the major equipment suppliers. The calculations proceed as follows:

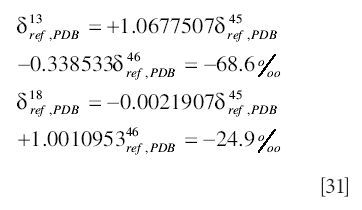
Then the erroneous step

from which it is deduced that

with, in this case, obvious error in the carbon result.

Concluding Remarks

When determining isotopic composition of a sample from an MS measurement, the practitioner must ensure that the method of calculation is understood properly and that the units used are stated clearly and coherently. In this tutorial, we have attempted to bring together the practices in common usage so that researchers new to this field can obtain a good understanding of the fundamentals involved. We do not claim that this is an exhaustive list of possible methods used in this field — for example, there are alternative methods of correction for ¹⁷O in CO₂ work to the Craig correction (11). However, we have attempted to explain those commonly encountered.

In some applications, deriving the isotopic composition of the sample is only the preliminary step. For example, in tracer work, it is then necessary to proceed to obtain tracer/tracee ratios for the sample (12), for which it is vital that the use of the appropriate units is understood (that is, isotopic versus fractional abundance). Beyond all these considerations, the savvy practitioner will also keep in mind that while the instrumentation is highly developed to detect relative differences in isotopic composition, the determination of absolute values is a very different matter. However, comfort can be taken by the commonly expressed view that "For all practical purposes this is of no consequence, though it is an interesting piece of scientific trivia" (13).

Modern MS equipment is supplied with sophisticated software in which many of the calculations described in this article are embedded. We would urge that all workers reliant upon the results from these machines (and not just the technical staff responsible for their operation) at least be familiar with the various scales used for quoting isotopic abundance, their limitations, and the approximations sometimes used in their derivation.

The next installment of this tutorial will explain state-of-the-art isotope application techniques such as mass isotopomer distribution analysis (MIDA) and position-specific isotope analysis (PSIA).

Note

† We have adopted the spelling "per mill" for the term meaning "per thousand" in accordance with the English edition of the International Standard ISO 31-0, Quantities and Units — Part 0: General Principals, sub-clause 2.3.3 (Reference number ISO 31-0:1992(E)).

Dietrich Volmer is Head of the Bioanalytical Sciences department at the Medical Research Council's Human Nutrition Research institute in Cambridge, United Kingdom. He is interested in different areas of biological mass spectrometry, including biomarkers, metabolomics, and structural elucidation techniques.

Les Bluck is a senior faculty member in Dr. Volmer's department, with strong interests in stable isotope tracer techniques and physiological modeling.

References

(1) J.T. Brenna, Mass Spectrom. Rev. 16(5), 227–258 (1997).

(2) A.E. Fallick, Stable Isotope Tracers for Metabolic Studies. SURRC Publications, SURRC (1986).

(3) C. Slater, et al., Stable isotopes and the international system of units. Meeting of the Stable-Isotope-Mass-Spectrometer-Users-Group (SIMSUG 2001), Glasgow, Scotland, John Wiley & Sons Ltd. (2001).

(4) L. Bluck and D.A. Volmer, Spectroscopy 23(10), 36–43 (2008).

(5) L. Bluck and D.A. Volmer, Spectroscopy 24(2), 50–57 (2009).

(6) M. Groning, et al., Intended Use of the IAEA Reference Materials. Part II: Examples on Reference Materials for Stable Isotope Composition. In The Use of Matrix Reference Materials in Environmental Analytical Processes. Cambridge, Royal Society of Chemistry (1999).

(7) H. Craig, Science 133(3467), 1833–1834 (1961).

(8) H. Craig, Geochim. Cosmochim. Acta 12, 133–149 (1957).

(9) A.L. Sessions et al., Anal. Chem. 73(2), 192–199 (2001).

(10) A. Prentice, Ed., The Doubly-labeled water method for measuring energy expenditure - Technical recommendations for use in humans. Vienna, International Atomic Energy Agency (1990).

(11) S.S. Assonov and C.A.M. Brenninkmeijer, Rapid Commun. Mass Spectrom. 17(10), 1007–1016 (2003).

(12) C. Cobelli, et al., Am. J. Physiol. 262(6), E968–E975 (1992).

(13) J.M. Hayes, Spectra 8, 3–8 (1982).

(14) L. Tornqvist, P. Vartia, et al., American Statistician 39(1), 43–46 (1985).