Statistics and Chemometrics for Clinical Data Reporting, Part I
This article describes the application of chemometric methods and statistics for reporting clinical quantitative measurement methods. The equations and terminology are consistent with the Clinical and Laboratory Standards Institute (CLSI) guidelines. These chemometric and statistical methods describe the accuracy and precision of a test method compared to a reference method for a single analyte determination. Part I will introduce these concepts and Part II will discuss the statistical underpinnings in greater detail.

This article describes the application of chemometric methods and statistics for reporting clinical quantitative measurement methods. The equations and terminology are consistent with the Clinical and Laboratory Standards Institute (CLSI) guidelines. These chemometric and statistical methods describe the accuracy and precision of a test method compared to a reference method for a single analyte determination. Part I will introduce these concepts and Part II will discuss the statistical underpinnings in greater detail.
Often there is confusion in multidisciplinary uses of statistical methods due to the variation in terminology, assumptions, and specific use of statistical methods within each scientific or technical discipline. An analytical chemist might look at analytical performance quite differently than a clinical chemist, or a physicist, or a mechanical engineer. An individual from one technical discipline might only be interested in overall error or deviation of one analysis method as compared to another reference method, whereas another individual might be more interested in bias and precision, and still another in tolerance stacking.

Howard Mark
In the interest of unification of multiple disciplines into a reasonable set of statistical parameters useful for analytical data evaluation, a group of individuals at Luminous Medical, Inc. (Carlsbad, California) decided to consolidate their efforts and combine analytical chemistry, clinical chemistry, bioengineering, physics, and biochemistry concepts into a single set of statistical parameters that would be useful and descriptive to a multidisciplinary team involved in looking at analytical method comparison (please refer to Acknowledgment section).

Jerome Workman
This column describes how to perform statistical analysis of quantitative measurement methods. The equations and terminology in this article are consistent with Clinical and Laboratory Standards Institute (CLSI) guidelines (1). These statistical analyses evaluate the accuracy of a test method compared to a reference method that measures the same analyte. References 2–6 yield multiple descriptions and worked problems associated with the individual statistics demonstrated in this article.
Definitions
A comparison of methods records differences between a test method and a comparative or reference method:
X comparative or reference method
Y test method
xi observation i from comparative method
yi observation i from test method
For clarity, this article assumes the comparative method is a traceable reference method that has better precision than the test method, which can be achieved by averaging replicate reference measurements if necessary.
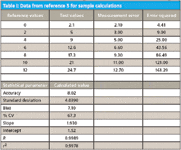
Table I: Data from reference 5 for sample calculations
Measurement Error
The Measurement Error (ei) is the test method measurement minus the reference method
e = Test Measurement – Reference Method
or equivalently, using the CLSI definitions, the measurement error for the for the ith observation is
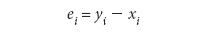
Accuracy
Accuracy includes both random and systematic components of a single measurement. Accuracy for a group of observations of the test method relative to the comparative method is calculated as
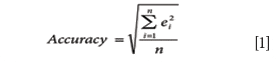
where n is the number of measurements. A common statistical term for this accuracy calculation is a root mean squared error (RMSE). Similar statistics are used to quantify errors in multivariate calibration and prediction, such as the root mean squared error of prediction (RMSEP, also known as SEP). Note: SEP = the square root of (SDr2 + Bias2).
Trueness and Bias
Trueness is the closeness in agreement between the average value from a series of measurements and a recognized reference method or traceable standard. The measure of 'trueness' is usually expressed in terms of bias (B)
Bias = average (Test Measurement) – average (Reference Method)
or equivalently, using the CLSI definitions
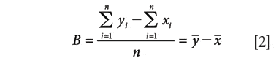
For more details on bias estimation and verification see references 1 and 4–6.
Precision
Precision is defined as the closeness of the agreement between the test measurement results under specified conditions. In general, medical device manufacturers report precision estimates for repeatability and reproducibility conditions. These are considered the extreme measures of precision. Repeatability (within-run precision) is the precision of measurements made by the same operator, using the same equipment, in a short period of time. Reproducibility (total precision) is assessed over multiple days and usually includes different operators and devices.
The simplest way to estimate repeatability is to compute the standard deviation (SD) of a sequence of repeat measurements on identical test material
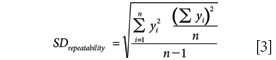
In blood samples the glucose level can change due to red blood cell metabolism. If these glucose changes are a significant contribution to the standard deviation then repeatability can be approximated from the measurement errors
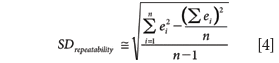
This is an approximation because the repeatability estimate now includes the imprecision of both the test method and the reference method.
The reproducibility (ST) of a measurement is a calculation that typically combines repeatability, between-run, and between-day standard deviations. The necessary calculations are included in CLSI Document EP5-A2 (1).
Precision (expressed in terms of repeatability and reproducibility) should be assessed at concentration levels that span the measuring range and include medical decision levels. The reported results should include the concentration level, number of samples, and precision. Precision should be reported in absolute units (such as mg/dL) and in relative units expressed as a coefficient of variation. The coefficient of variation expresses the precision relative to the average reference value (x{?i ).
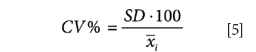
Sample Data Calculations
The sample calculations use data from Reference 5 for comparison.
Computation of the Regression Line
Pearson Product-Moment Correlation Coefficient (r)
The Pearson product-moment correlation coefficient for x and y data pairs is the alikeness of x to y including their respective differences ratioed to the dispersion (standard deviation) of the dataset. So the same error between x and y computes to a higher correlation when the data is more disperse or has a wider range. Therefore to compare correlation between experiments one should use the same data distribution for both. A high correlation does not mean smaller error unless the spread of the data used in the experiments is equivalent.
The correlation coefficient computed using a standard summation notation is defined as:
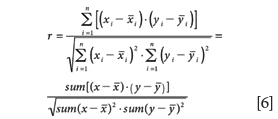
Coefficient of Determination (R2 )
The Coefficient of Determination, R2, is the square of the Pearson product-moment correlation coefficient. This statistic represents the amount of variation in the data that is modeled by linear fit of the test and comparative data pairs as a fraction of 1.0.
Note: For a multivariate calibration, this statistic is often termed the coefficient of multiple determination. It specifically reports the total amount of variation in the data that is fully modeled by the calibration equation as a total fraction of 1.0. If the R2 is 1.00 then 100% of the variation is modeled in the calibration; similarly, an R2 of 0.80 indicates 80% of the variation has been modeled using the mathematics selected.
Slope (m0)
This is the slope of the regression line between x and y paired values. A slope of 1.00 indicates perfect agreement between a change in reference value magnitude and a change in test value magnitude. This slope value does not indicate the magnitude of the bias or of the intercept of the regression line between x and y values. It is computed as follows (summation notation is indicated):
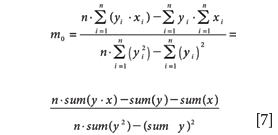
y-Intercept (i)
The y-intercept is the point on the y-axis where the regression line crosses the 0 reference (x) value. It is not the bias which has already been defined as Parameter #3. In summation notation the intercept is computed as follows:
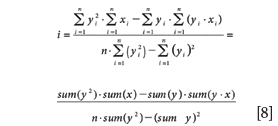
Acknowledgment
The column editors would like to thank Drs. Bill Patterson, Shonn Hendee, Stephen Vanslyke, and David Abookasis of Luminous Medical for their multidisciplinary contributions in authorship, review, and editing for this discussion of statistical methods suitable for clinical data presentation when comparing different methods of analysis.
Howard Mark serves on the Editorial Advisory Board of Spectroscopy and runs a consulting service, Mark Electronics (Suffern, NY). He can be reached via e-mail: hlmark@prodigy.net
Jerome Workman, Jr. serves on the Editorial Advisory Board of Spectroscopy and is currently with Luminous Medical, Inc., a company dedicated to providing automated glucose management systems to empower health care professionals.
References
Many references are available. These have been selected as they are specifically related to the use of data for spectroscopy, and for comparison of general analytical methods.
(1) Clinical and Laboratory Standards Institute (CLSI) guidelines: Q300-001, Terminology for standard definitions. For more details on statistical estimation and verification see:
- CLSI Document EP5-A2, Evaluation of Precision Performance of Quantitative Measurement Methods; Approved Guideline — Second Edition.
- CLSI Document EP10-A2, Preliminary Evaluation of Quantitative Clinical Laboratory Methods; Approved Guideline — Second Edition.
- CLSI Document EP15-A2, User Verification of Precision and Trueness; Approved Guideline — Second Edition.
- CLSI Document EP9-A2, Method Comparison and Bias Estimation using Patient Samples; Approved Guideline — Second Edition.
- CLSI Document EP10-A2, Preliminary Evaluation of Quantitative Clinical Laboratory Methods; Approved Guideline — Second Edition.
- CLSI Document EP15-A2, User Verification of Precision and Trueness; Approved Guideline — Second Edition.
(2) ASTM Standard Practice E1655-00, "Standard Practices for Infrared, Multivariate, Quantitative Analysis," American Society for Testing and Materials International, Barr Harbor Dr., West Conshohocken, PA 19428.
(3) N.M. Faber, F.H. Schreutelkamp, and H.W. Vedder, Spectroscopy Europe 16(1), 17–20 (2004).
(4) W.J. Youden and E.H. Steiner, Statistical Manual of the AOAC, 1st Ed. (Association of Official Analytical Chemists, Washington, D.C., 1975).
(5) J.C. Miller and J.N. Miller, Statistics for Analytical Chemistry, 2nd Ed. (Ellis Horwood, New York, 1992).
(6) H. Mark and J. Workman, Chemometrics in Spectroscopy (Elsevier/Academic Press, Boston, 2007), chapters 58–61.
