Theoretical and Experimental Investigation of the Electronic Spectra of Antitumor Compounds

The study of photophysical properties of heterocyclic organic molecules has achieved considerable importance recently because many of these molecules form an integral part of biologically important compounds and have various uses. Substituted 2-arylbenzothiazoles, although having industrial and commercial uses as fluorescence whitening agents (1), photoconducting materials (2), and as herbicides in agriculture, have not received much attention.

In the last few years, benzoxazoles and related heterocycles benzimidazoles and benzothiazoles were studied extensively for their antitumor, antiviral, and antibiotic properties as the new nonnucleoside topoisomerase I poisons, HIV-1 reverse transcriptase inhibitors, and potent DNA gyrase inhibitors (3–7).

The biochemical reactivity of a drug is a direct consequence of its electronic structure, which manifests itself in several ways. The most straightforward manifestation occurs in the electronic absorption spectra. This manifestation enables the detailed understanding of the forces that govern the electronic structure of the studied molecules. The following article presents a comparative investigation of the electronic absorption spectra of the studied benzazole, 2-phenyl benzazole, and 2-(4-aminophenyl)benzazole. .

The studied compounds possess two positions that can accept protons, with a subsequent delocalization of the charge, (see Figure 1) and one or two sites that can donate protons to the solvent. Thus the spectral shifts observed depend upon the preferential interaction of the solvents with the solute molecule. The solvent effect thus needs to be investigated thoroughly and analyzed.

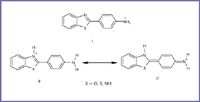
Figure 1. The studied compounds have two positions that can accept protons with a subsequent delocalization of the charge, and one or two sites that can donate protons to the solvent.

The spectra of large organic molecules usually are very difficult to interpret because most electronic transitions are observed as broad diffuse bands. Computer-deconvolution of these bands therefore is essential. However, theoretical computation of the spectra of the drugs under investigation is essential to get a quantitative understanding of the ground and excited state properties and their polarizabilities. This can be done efficiently either using semiempirical methods specially parameterized to reproduce experimental spectra, such as the ZINDO/S method, or by using the time-dependent density functional theory (TDDFT) method, which is the most widely applicable method nowadays (8–13).

In the present study, the electronic absorption spectra of some benzazoles, 2-phenylbenzazoles, and 2-(4-aminophenyl)benzazoles were measured in different solvents and calculated theoretically at the TDDFT/B3LYP/6-31G** level of theory. Results are compared with those obtained by the semiempirical ZINDO/S method, which is designed and parameterized to reproduce experimental electronic spectra. Analysis of the charge density distributions and relative polarities of the ground and excited states will enable quantitative understanding of the observed solvent effects.

The present study is in fact a part of a major project aimed at the development of a quantitative structure–activity relationship (QSAR) for the series of antitumor drugs under investigation. All structure-determining factors will be accounted for in the QSAR study.

Method of Calculation

All calculations were performed using the G98 (14) package of programs. The ground-state structures were optimized at the B3LYP (15)/6-31G** level. TDDFT and ZINDO/S were used to calculate the excitation energies and electronic spectra. The electron-density distributions of the molecular orbitals involved in the electronic transitions were mapped using the hyper chem.V

_6.01

software package, which operates in a Microsoft Windows environment. Computer deconvolution of the experimental spectra was performed using Mathcad 7.0 Plus (16) software.

Experimental

Solvents.

All solvents used in the present work were BDH spec quality, which were used without any further purification.

Compounds. All the studied compounds (APBO, APBT, APBI) were prepared and purified as reported in the literature (17) (see Figure 2).

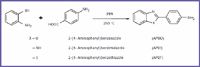
Figure 2. All the studied compounds (APBO, APBT, APBI) were prepared and purified as reported in the literature (17).

Apparatus. All absorption spectra reported in this work were measured using a JASCO UV-530 Spectrophotometer through the wavelength 2.48–7.44 eV using 1.0-cm cells.

Results and Discussion

Electronic spectra of benzazole and 2-phenyl benzazole.

It is interesting to examine the electronic spectral characteristics of benzazoles before we discuss that of the composite systems under investigation. Table I presents the experimental and theoretical spectra of benzimidazole (23), benzoxazole (20), and benzothiazole (22). In the case of benzoxazole, the first absorption band centered at ~3.42 eV is derived from the B

_2u

benzene system, and shows its characteristic fine vibration structure. The moderate bathochromic shift and intensification relative to the benzene system at 3.16 eV is a normal result of weak conjugation of the heteroatoms with the phenyl ring. This broad band, which spans the region 3.47-3.1 eV, was attributed experimentally to one transition, the B

_2u

system of the benzene moiety.

Theoretical calculation of the spectrum of benzoxazole, however, shows two main band systems in this region, the first centered at 3.56 eV with moderate to weak intensity and a much stronger transition centered at 3.16 eV. The first, S₁, is a (π, π*)¹ state composed of three main configurations: φ_-1φ₁, φ_-1φ₂, and φφ₂. The second, S₂, (π, π*)¹ state centered at 3.16 eV, is composed of two main transitions: φφ₁ and φφ₂. It is interesting to note that these two configurations are the major components of S₁. Both (π, π*)¹ states involve transitions from the molecular orbital φ which is localized on the benzene ring. On the other hand, the delocalization of φ₁ and φ₂ indicate clearly that S₁ and S₂ are transitions localized on the benzene ring perturbed to some extent by the heteroatom system.

It should be noted that while ZINDO/S reproduced the experimental spectra fairly well, the TDDFT method reproduced the right order and origin of S₁, S₂, and S₃ although the correspondence between the computed and experimental transition energies is not satisfactory. The TDDFT computations underestimate the wavelength of all states by 0.37 eV.

Replacement of the O-heteroatom by NH does not introduce any appreciable changes in the extent of conjugation or polarization of the electronic spectra. Thus, the electronic absorption spectra of benzimidazole are very much similar to that of benzoxazole. Results of the present work confirm that the TDDFT approach underestimates the position of all transitions. The magnitude of this underestimation amounts to 0.37 eV, as in the case of benzoxazole.

Four overlapping band systems are observed in the spectrum of benzothiazole at 3.65, 3.53, 3.12, and 2.68 eV. The ZINDO/S computation reproduced the experimental spectrum fairly well. Results are presented in Table I. The first (π, π*)¹ state is a delocalized transition involving the whole π system. The involvement of the S-atom p_π orbitals in conjugation seems more pronounced in the case of benzothiazole than O- or NH conjugation.

TDDFT/B3LYP/6-31G** computations of the spectrum of benzothiazole follow the same trend observed in the case of benzoxazole and benzimidazole in that they underestimate considerably the position of electronic transitions by ~0.42 eV. Moreover, the separation between S₂ and S₃, which is observed to be 0.41 eV and predicted by ZINDO/S to be 0.18 eV, is reduced appreciably in TDDFT calculation to 0.04 eV only.

Table II presents a comparison between the experimentally observed and theoretically computed spectra of the 2-phenyl benzoxazoles studied in the present work as compared with benzoxazoles the phenyl derivatives show, as a general trend, considerable red shift and intensification of the first (π, π*)¹ state. This would suggest extended conjugation over the entire molecular framework. In the case of 2-phenylbenzoxazole, the ZINDO/S calculated transition energy for the first (π, π*)¹ state is in good agreement with the experimental value. Both methods assigned this state to HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) transition as a major configuration. This elaborates upon our assumption that this molecule enjoys considerable π–conjugation extended over the whole molecular framework. The same general agreement holds in the case of 2-phenylbenzothiazole where the ZINDO/S calculations agree well with the experimental transition energy for the first (π, π*)¹ excited state and in its assignments to a major configuration involves a HOMO–LUMO transition.

It should be noted at this point that the first (π, π*)¹ state in all the 2-phenylbenzazoles studied are much less polarized than that of the corresponding states in benzazoles. This would suggest that the TDDFT approach underestimates the position of highly polarized excited states.

This underestimation decreases as the polarization of the excited state decreases. In the case of transitions that involve no charge transfer (CT) character, TDDFT predicts transition energies in the same quality as that predicted by ZINDO/S and are in good general agreement with the experimental spectra.

The electronic spectra of 2-(4-aminophenyl)benzimidazole (APBI). Figure 3 presents the electronic absorption spectra of APBI in different solvents. The spectrum in ethanol shows four diffuse and broadband systems, centered at 3.97 eV, 3.6, 3.21, and 2.6 eV. The high extinction coefficient, and red shift of λ_max with increasing solvent polarity, confirm the π–π* nature of these transitions. The small blue shift observed in water relative to methanol or ethanol indicates that water is acting as a better hydrogen donor solvent to the ion pair of the amino group rather than a hydrogen acceptor.

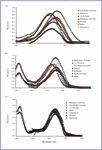
Figure 3. Electronic absorption spectra of (a) 2-(4 aminophenyl)benzimidazole, (b) 2-(4-aminophenyl)benzothiazole), and (c) 2-(4-aminophenyl)benzoxazole.

The two normal band systems of benzimidazole molecule (3.45, 3.73, L_b; 3.01 eV, L_a) are kept intact except that both are red shifted (3.97, 3.94, 3.6 eV, L_b; 3.43, 3.32, 3.21 eV, L_a), whereas the third band system, which, in the case of benzimidazole, is observed in the 210 eV region with a considerable vibrational structure, appears in almost the same position in the case of APBI yet the detailed fine structure is lost.

Table III presents a comparison between the experimental spectrum and that computed theoretically using ZINDO/S and TDDFT methods. The TDDFT theoretically computed spectra of APBI predicts three (π, π*) states at 300.6, 278.5, and 3.32 eV, while ZINDO/S predicts three (π, π*) states at 320.9, 292.9, and 285.5 eV.

The first is a long wavelength transition at 320.9 eV, which is in excellent agreement with experimentally observed value (320 eV). This excited state is a (π, π*) and is a mixture of three main configurations: φ_-1φ, φ_-1φ₂, and φ_-3φ₂. The HOMO–LUMO transition seems to dominate this state (~40%). This configuration is localized largely on the phenyl ring with a little contribution from the heterocyclic moity (see Figure 4). Therefore, this transition opposes the dipole moment vector and hence the S₁ state is less polar than the ground state. This would suggest that the first (π, π*) excited state would show slight red shift upon increasing solvent polarity.

Figure 4. Representation of the charge density distributions of the frontier orbitals involved in ZINDO/S calculation for 2-(4-aminophenyl)benzimidazole.

The first (π, π*)¹ singlet state of APBI is predicted by TDDFT at 3.72 eV in a less satisfactory agreement with ZINDO/S and experimental spectra (3.97 eV). However, TDDFT agrees with ZINDO/S in the assignment of this band to a HOMO–LUMO transition as a dominating ~40% configurations and also agrees with the polarization changes predicted by ZINDO/S. This is in agreement with the conclusion drawn by Parac and Grime (18) that TDDFT the approach shows strongly size system dependent error for the low-lying π–π* excited states. In the present case, this error is an overestimation of the excitation energy of the first π–π* state amounts to 0.25 eV.

The two normal band systems of APBI are observed at 3.45 and 3.37 eV (19) and predicted theoretically by ZINDO/S at 3.63 and 3.53 eV; TDDFT, on the other hand, predicts these two transitions at 278.5 and 269.97 in excellent agreement with the experiment. These bands correspond to S₂ and S₃ states.

In the case of ZINDO/S calculations, the second (π, π*) 1 excited state is a mixture of the φ_-4φ₂ and φ_-1φ₁. The later configuration involves an intramolecular CT from the heterocyclic moiety into the phenyl ring, whereas the φ_-4φ₂ configuration is a transition localized on the phenyl ring. This contribution manifests itself as a perturbation only to the main configuration φ_-1φ₁. The third (π, π*) excited state is composed of a major configuration φ_-1φ₂. Both molecular orbitals are more or less delocalized over the entire molecule. Thus, the third state (S₃) (π, π*) transition is a delocalized transition involving the entire molecule. S₂ and S₃ states are less polar than the first and the ground states, which explain the sensitivity of their positions to solvent polarity.

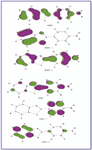
Figure 5. Representation of the charge density distributions of the frontier orbitals involved in ZINDO/S calculation for 2-(4-aminophenyl)benzothiazole.

TDDFT/B3LYP/6-31G** computed spectrum is presented together with the experimental data in Table III. Careful inspection of the data presented in this table reveals the following:

• The general features of the spectrum computed by TDDFT resembles those predicted by ZINDO/S calculations; it shows a long wavelength absorption at 3.72 eV and two short wavelength bands at 3.45 and 3.34 eV.

• The first (π, π*)1 excited state (S₁) is composed of a major configuration φ_-1φ, that corresponds to a HOMO–LUMO transition (¹L_a).

• The second (π, π*)¹ excited state is a combination of two configurations, namely φ_-4φ and φ_-1φ₁. φ_-1φ₁ dominates to a large extent, which corresponds to HOMO–LUMO+1 (¹L_b) transition (21).

• The third (π, π*) excited state is a combination of φ_-2φ, φ_-1φ₁, φ_-1φ₂, and φ_-1φ₃ configurations. The weight of the former is much greater (~40%). This configuration corresponds to HOMO-1–LUMO transition. Surprisingly, the S₂ and S₃ states always are much less polar than the ground state.

• Finally, the ¹L_b transition exhibits a weak intensity as compared to that of the L_a state. Since the states are close in energy (L_a= 4.12 eV, L_b= 4.59 and 4.45 eV), the ¹L_b state is very often hidden under the more intense ¹L_a band and therefore difficult to detect experimentally.

• It is worth noting that TDDFT was superior to ZINDO/S in predicting the excitation energies of S₂ and S₃ and also their separation.

The Electronic Spectra of APBO and APBT. Tables IV and V present the experimental and the theoretically computed spectra of APBT and APBO. The similarity of the spectra of APBT and APBO with their respective phenylbenzazole, the type of molecular orbital contributions, and its polarization indicate that the lowest energy transitions in these molecules are of the π–π* character and reflects the extended conjugation in these molecules.

Figure 6. Representation of the charge density distribution of the frontier orbitals involved in ZINDO/S calculation for 2-(4-aminophenyl)benzoxazole.

The red shift in the longest wavelength band of (APBT or APBO) as compared to that of benzazole and 2-phenylbenzazole, can be explained by the charge transfer interaction of NH₂ group with aromatic moiety. Figures 3b and 3c present the electronic absorption spectra of APBT (3b) and APBO (3c), in different solvents.

Although the general features of these spectra do not differ much from those of the spectrum presented before for APBI, the observed bands in the spectra of APBT and APBO are red shifted and intensified as compared to those observed in the spectrum of APBI. In fact, the general features, peak position, and intensities of the spectrum of APBT resemble those of APBO to a striking extent. The theoretically computed spectra (TDDFT and ZINDO/S) of APBT and APBO are presented and compared with the experimental spectra in Tables IV and V, respectively.

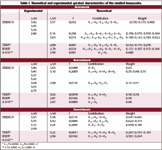
Table I. Theoretical and experimental spectral characteristics of the studied benzazoles.

The assumption made by Passarini (20) that the phenyl moiety in the studied composite compounds acts as the main chromphore is not entirely correct. The present molecular orbital calculations indicate clearly that the first (π, π*)¹ excited state in the spectra of APBT and APBO is a delocalized state involves the entire molecular framework. These (π, π*)¹ states are composed of a major configuration that involve the HOMO–LUMO transition. APBT show its first (π, π*)¹ state at a longer wavelength than that of APBO. This (π, π*)¹ state show red shift by increasing solvent polarity indicating that it is more polar than the ground state.

ZINDO/S and TDDFT computations of the spectra of APBT and APBO failed to reproduce the experimental spectra satisfactory. One may note the following:

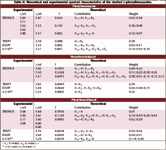
Table II. Theoretical and experimental spectral characteristics of the studied 2-phenylbenzazoles.

Both theoretical models predict the first (π, π*)1 state at ~3.97 eV where it is assigned to a major configuration involving a HOMO–LUMO transition. The HOMO's of both APBT and APBO are delocalized over the entire molecular framework. The LUMO, on the other hand, although delocalized, yet its weight on the amino-phenyl moiety is relatively larger. Thus, the two theoretical models used in the present study indicate that the first (π, π*)¹ state is a delocalized transition involving CT character onto the aryl ring. The second (π, π*)¹ state in the spectra of APBT is predicted theoretically at ~3.62 eV. This state involves three configurations where φ_-1φ₁ configuration has the major contribution. φ_-1φ₁ is a CT configuration involves migration of the charge density onto the phenyl ring from both the benzoxazole moiety and from the amino group. In the case of APBO, the second (π, π*)¹ state is predicted theoretically at ~3.62 eV by ZINDO/S. However, TDDFT calculated spectra of APBO show a general blue shift of 0.25 eV as compared with that predicted by ZINDO/S. This is true for the two highly polarized excited states S₁ and S₂.

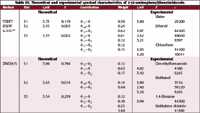
Table III. Theoretical and experimental spectral characteristics of 2-(4-aminophenyl)benzimidazole.

Summary and Conclusion

The present study presents an investigation of the experimentally observed spectra of a series of biologically important class of compounds, namely, 2-(4-aminophenyl) benzoxazoles. The observed spectra of these antitumor drugs are highly solvent-dependent and diffuse, so that complete and thorough analysis using computer deconvolution and molecular orbital computations were essential. Comparison with the spectra of benzazoles and 2-phenylbenzazoles facilitate the understanding of the origin and the assignment of the observed band systems. The main molecular orbital method used in the present work for calculating the electronic spectra is the ZINDO/S method; this method is well known to give theoretical spectra in very good agreement with the corresponding experiment. The present work provides the opportunity to test the TDDFT method, which is a new abinitio approach to calculate the electronic spectra.

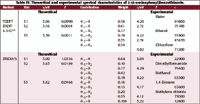
Table IV. Theoretical and experimental spectral characteristics of 2-(4-aminophenyl)benzothiazole.

The following conclusions can be drawn from the results of the present study:

• For all of the studied compounds, both the ZINDO/S and the TDDFT calculated transition energies for the first (π, π*)¹ state are in good agreement with the experimental value. Both methods assigned this state to a HOMO–LUMO transition as a major configuration. This elaborates upon our assumption that these molecules enjoy considerable π-conjugation extended over the whole molecular framework.

• In the case of transitions that involve no CT character, TDDFT predicts transition energies in the same quality as that predicted by ZINDO/S and are in good general agreement with the experimental spectra.

• In the case of APBI, the ¹L_b transition exhibits weak intensity as compared to that of the L_a state. Since the e states are close in energy, the ¹L_b state is very often hidden under the more intense ¹L_a band and therefore difficult to detect experimentally.

• In the case of APBI, it is worth noting that TDDFT was superior to ZINDO/S in predicting the excitation energies of S₂ and S₃ and also their separation.

• The HOMO's of both APBT and APBO are delocalized over the entire molecular framework. The LUMO, on the other hand, is delocalized, although its weight on the amino-phenyl moiety is relatively large. Thus, the two theoretical models used in the present study indicate that the first (π, π*)¹ state is a delocalized transition involving CT character onto the aryl ring.

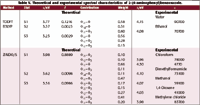
Table V. Theoretical and experimental spectral characteristics of 2-(4-aminophenyl)benzoxazole.

References

1. E. Belgoderr, R. Bossio, S. Chimichi, V. Parrini, and R. Pepino,

Dyes Pigm.

4

, 59 (1983).

2. Kalle& Co., A.G., Br. Patent 895001, April 26, (1962).

3. L.Perrin, A. Rakik, S.Yearly, C. Baumberger, S. Kinloch-de Loies, M. Pechiere, and B. Hirschel, AIDS10, 1233 (1996).

4. S. Staszewski, J. Infect Dis. 171, 1159 (1995).

5. D.B. Olsen, S.S. Carroll, J.C. Culberson, J.A. Shafer, and L.C. Kuo, Nucleic Acids Res. 22, 1437 (1994).

6. Q. Kim, J.S. Sun, B. Gatto, C. Yu, A. Liu, L.F. Liu, and E.J. La Voie, Bioorg. Med. Chem.4, 621 (1996).

7. C. Hubschwerlen, P. Pflieger, J.L. Specklin, K. Gubernator, H. Gmunder, P. Angehrn, and I. Kompis, J. Med. Chem.35, 1385 (1992).

8. E.K.U. Gross, J.F. Dobson, and M. Petersilka, in Density Functional Theory II, Springer Series in Topics in Current Chemistry, Band 181, R.F. Nalewajski, Ed. (Springer, Heidelberg, Germany, 1996).

9. M. E. Casida, in Recent Advances in Density Functional Methods, Band I, D.P. Chong, Ed. (World Scientific, Singapore, 1995).

10. C. Jamorski, M.E. Casida, and D.R. Salahub, J. Chem. Phys.104, 5134 (1996).

11. R. Auernschmitt and R. Ahlrichs, Chem. Phys. Lett.256, 454 (1996).

12. A. G�ng, H.H. Heinze, S.P. Ruzankin, M. Staufer, and N. R�, J. Chem. Phys.110, 2785 (1999).

13. F. Furche, J. Chem. Phys. 114, 5982 (2001).

14. M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, V.G. Zakrzewski, J.A. Montgomery Jr., R.E. Stratmann, J.C. Burant, S. Dapprich, J.M. Millam, A.D. Daniels, K.N. Kudin, M.C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G.A. Petersson, P.Y. Ayala, Q. Cui, K. Morokuma, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J. Cioslowski, J.V. Ortiz, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P.M. W. Gill, B. Johnson, W. Chen, M.W. Wong, J.L. Andres, C. Gonzalez, M. Head-Gordon, E.S. Replogle, and J.A. Pople, Gaussian, Inc., Pittsburgh PA, 1998.

15a. C. Lee, W. Yang, and R.G. Parr, Physical ReviewB37, 785 (1988). 15b. B. Miehlich, A. Savin, H. Stoll, and H. Preuss, Chem. Phys. Lett.157, 200 (1989).

16. Mathcad Plus 7.0, 1986-1997 Mathsoft Inc.

17. D.W. Hein, R.J.Alheim, and J.J. Leavitt, J. Am. Chem. Soc.79, 427 (1957).

18. M. Parac and S. Grime, Chem. Phys.292, 11 (2003).

19. A.K. Mishra, and S K. Dogra, Bull. Chem. Soc. Jpn.58, 3587 (1985).

20. R. Passarini, J. Chem. Soc. 2256 (1954).

21. J.R. Platt, J. Chem. Phys. 17, 484 (1949).

22. A. Cerniani and R. Passarini, J. Chem. Soc. 2261 (1954).

23. Steck, Nachod, Ewing, and Gorman, J. Am. Chem. Soc.70, 3406 (1948). n

Rifaat Hilal is with the chemistry department of Cairo University (Cairo, Egypt). E-mail: rhhilal@hotmail.com.

Ahmed A. Abdel Khalek and Shabaan A. K. Elroby are with the chemistry department of Cairo University, Beni-Seuf branch.