Density Functional Model of Raman Spectra for the Seminiferous Tubules of Hindlimb Unloaded Mice

A model Raman spectrum was constructed by using density functional theory (DFT) to track amino acid changes in the seminiferous tubules of hindlimb unloaded (HU) mice. A B3LYP functional with 6-31G* polarization basis sets were used in the calculations. A number of features in the model were comparable to the experimentally obtained spectrum collated with a 785-nm laser from the testicular tissues of the male mice unloaded for two weeks. A comparison of the theoretical and the experimental Raman spectra indicated that hydroxyproline and tryptophan are the major amino acids in the seminiferous tubules. By using Raman spectroscopy, we also confirmed by histological measurement that the same molecules showed depression. The changes in these molecules resulted in the disruption of the testicular seminiferous tubules, resulting in pathological conditions such as epithelial atrophy, tubular shrinkage, and lumen expansion. Our observations indicated that the DFT model of the Raman spectra has the potential to precisely predict and analyze the features of the experimental spectra in the testicular tissues of HU mice.

Amino acids can be found in varying quantities in different proteins (1). The structure and dynamics of various amino acids have been studied extensively through the use of Raman spectroscopy (2). The majority of the studies have been conducted on analytical grade samples of the individual amino acids. The literature is devoid of studies that discuss the composite spectrum of amino acids that are directly obtained from biological tissue. The composite Raman spectrum would not only be influenced by all the amino acids present in a biological specimen, but it would also highlight their interactions. Therefore, the goal of this study was to gain insight into the resultant spectrum of amino acids from the biological samples by conjoining the theoretical and experimental Raman spectroscopic techniques.

Raman spectroscopy detects the vibrational frequencies of several types of organic molecules. More recently, Raman spectroscopic techniques have also been applied to determine the structure, function, and properties of proteins (3), including amino acids (4–7) and for cancer diagnosis (8,9). Although the characteristic peaks (10–13) in the spectroscopic data of the biological samples denote the vibrational frequencies of specific molecules, the interpretations of the spectra in the literature are not consistent (8,14), which is partly because the biological objects are intrinsically variable and present a serious challenge in interpreting the Raman spectra. For example, protein molecules adopt different spatial structures and geometries in various conditions, and each geometry has its own unique vibrational fingerprint. Therefore, the experimental spectrum is the cumulative fingerprints of all spatial molecular variants of a molecule. Furthermore, a low-energy molecular configuration is more stable than a high-energy one, indicating that not all variants of a molecule are equally represented in a spectrum. This structural variation poses a significant problem for the characterization of molecules through spectroscopic techniques. The vibrational modes can be of several types depending on the molecular structures, conformations, and the frequency at which these modes occur and the Raman bands from different molecular components overlap, thus creating further difficulties in the identification process.

The problem of interpreting overlapping vibrational frequencies because of various amino acids and their conformations in biological samples can potentially be resolved by calculating the theoretical Raman spectra. In density functional theory (DFT) calculations, the choice of exchange and correlation functionals, coupled with the basis sets, plays a vital role in these calculations. In the modeling of biological systems, the Becke, three-parameter, Lee–Yang–Parr (B3LYP) functional is the most common because it gives an accurate description of hydrogen-bonded systems (15,16). The choice of the basis sets to accompany the functionals depends on the molecular system. Some examples of basis sets include 6-311++G(*,*) (17), aug-cc-pVTZ (5), aug-cc-pVDZ (4), 6-311++G(d,p) (18), and 6-31 + G(d) (6). This study examined whether the computed spectrum can be used to accurately identify amino acids when compared to the measured spectrum of a biological sample. Earlier, we characterized several signature molecular changes in the skeletal muscles of hindlimb unloaded (HU) mice by Raman spectroscopy (19), which were in agreement with the previous reports about the unloaded muscles (20). We further extended our findings by collecting the experimental Raman spectra from the testes of the HU and ground-based control mice to show that a sustained impairment in the blood flow to the testes does impact the early stages of spermatogenesis and can lead to testicular malfunction.

Materials and Methods

The experimental details about the HU mice conditions are previously described by us in the literature (19). The male mice were maintained under pathogen-free conditions, with 2–3 mice housed per cage (control) or one mouse per cage (unloaded) in a 12:12 (light:dark) cycle and provided with food and water ad libitum, as previously described in the literature (21). All mice were 16–18 weeks old at the start of the experiments. One group of mice was suspended for HU, whereas the other group was kept as the ground-based controls for 21 days. Following this, the mice were euthanized via cervical dislocation, and the testes tissues were collected from the HU and control mice (N = 5–6/group) for Raman spectroscopy and histological analysis.

In Raman spectroscopic experiments involving biological tissues, the first important parameter that is always considered is the selection of a laser that had an appropriate wavelength. Because of phonon–photon interactions, the intensity of the Raman signal is inherently very weak. Furthermore, the Raman scattering intensity is inversely proportional to the fourth order of the illuminating wavelength, implying that at longer wavelengths, the intensity of the Raman signals would drop dramatically. Therefore, Raman signals are suppressed by the higher noise level and by the decreased sensitivity if obtained using laser sources of wavelengths higher than 800 nm. This limitation has previously been reported in several studies (22). On the other hand, illumination by the shorter wavelength (405 nm or 532 nm) causes the materials to generate fluorescence, which hides the Raman peaks. We avoided these shortfalls by using a 785-nm laser, which offers an optimal balance between the scattering efficiency and the influence of fluorescence.

The experimental Raman spectra were obtained by using a Renishaw Raman spectrometer. Three specimens were selected for the control and the HU testes. A set of 10 spectra were collected from various locations of each sample to obtain the average spectrum. In each recording, the site of a specimen was exposed for 10 s to a 785-nm wavelength laser with a spot size of 50 μm and a laser power of 1%. The spectral range was kept between 100 cm^-1 and 1200 cm^-1, which represents the fingerprint region for finding signature peaks from the biological molecules. To avoid damage to the testes tissues from the intensity of the laser, the spectra were collected at intervals of 500 cm^-1 before being stitched together to obtain the full spectrum.

Typically, the experimentally obtained spectra exhibit Mie scattering and the Raman vibrational peaks are not clearly visible. To resolve the peaks contributed by each molecule in the sample, the frequencies and the intensities of the spectra were fitted with the Lorentzian function (23) by using a commercial computer program (24). The Lorentzian peak function has a bell shape and much wider tails than the Gaussian function and is defined by equation [1] below:

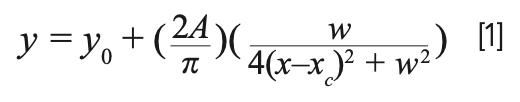
The parameters y₀, x_c, w, and A represent the offset, center, full width at half maximum (fwhm), and the area of a peak, respectively.

Our analysis shows that the hydroxyproline and the tryptophan are the major molecular constituents of the testes in addition to unraveling several novel molecular changes in the mouse testes under HU conditions. For the histology, the testes tissues were fixed in Bouin’s solution and stored in 70% ethanol, followed by paraffin embedding. The tissues were then sectioned at 4 μm slices and further stained with hematoxylin and eosin for light microscopic examination, as described in the literature (25). Morphometric analysis for the architecture of seminiferous tubules, as well as tubular diameter, epithelial height and luminal diameter, were performed following the procedure described in the literature (26).

Theory and Calculations

A model of the theoretically generated Raman spectra was constructed by performing energy calculations within DFT on the isolated single amino acid molecules in their electronic ground state in the gas phase. The DFT calculations were based on the assumption that the exact energy may be expressed as a function of electron density. In this work, we used the B3LYP functional, which combined Slater, Hartree–Fock, and Becke exchange with the correlation terms because of Lee, Parr, and Yang. It is a global hybrid generalized gradient approximation functional (GH-GGA), which was applied to determine the electronic structure of biological systems (16). A 6-31G* polarization basis set was chosen for the density functional models. A molecular vibration is Raman active if it changes the polarizability of the molecule. Therefore, the B3LYP functional with 6–31G* polarization basis sets was considered the most suitable approximation to calculate the Raman spectra for biological systems. All calculations were performed by using the Spartan ‘18 Parallel Suite version 1.3.0 software (27).

Results and Discussion

The unloading of the mice resulted in a characteristic disruption of the testicular architecture under the light microscope as shown in Figure 1.

FIGURE 1: (a,b) Changes in the testicular architecture in the hindlimb of unloaded mice.

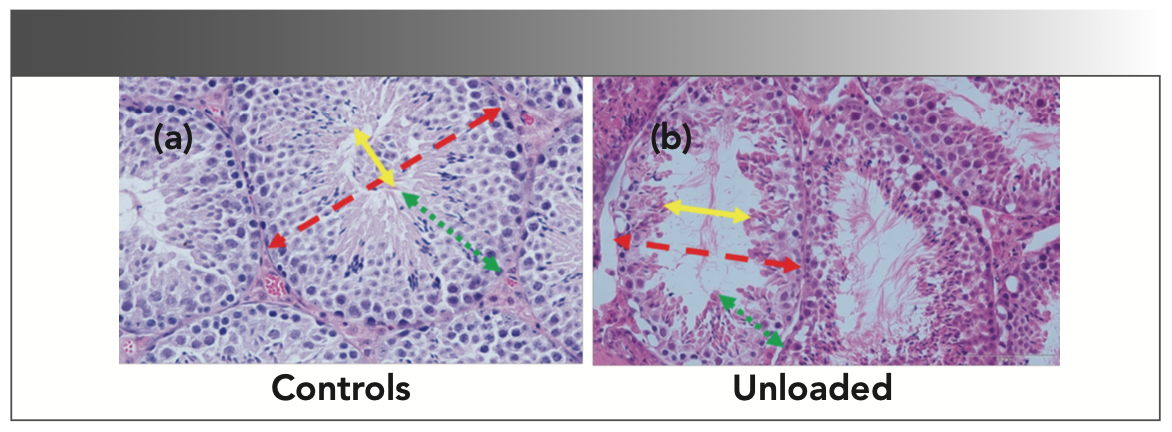
The unloading was associated with epithelial atrophy (green arrows), a reduction in the tubular diameter (red arrows), and an expansion of the luminal diameter (yellow arrows) in the seminiferous tubules.

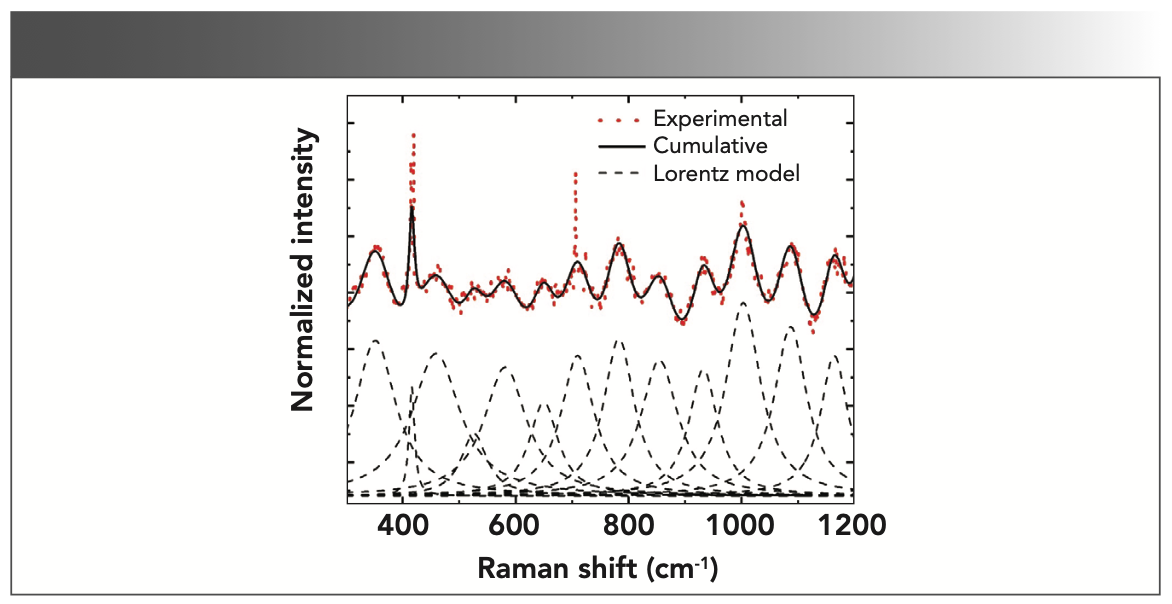
The experimental Raman spectrum from a representative control testes sample is shown in Figure 2. The experimental spectrum (red dots) was fitted with the Lorentz fit (black dashes) to obtain the cumulative spectrum (solid black) to resolve the Raman peaks. The cumulative spectrum clearly shows the vibrational bands at 351 cm^-1, 416 cm^-1, 459 cm^-1, 526 cm^-1, 581 cm^-1, 650 cm^-1, 710 cm^-1, 782 cm^-1, 854 cm^-1, 932 cm^-1, 1003 cm^-1, 1087 cm^-1, and 1164 cm^-1.

FIGURE 2: Experimental Raman spectrum (red dots), the Lorentz fit (black dashes), and the cumulative fit of each Lorentz peak (black solid).

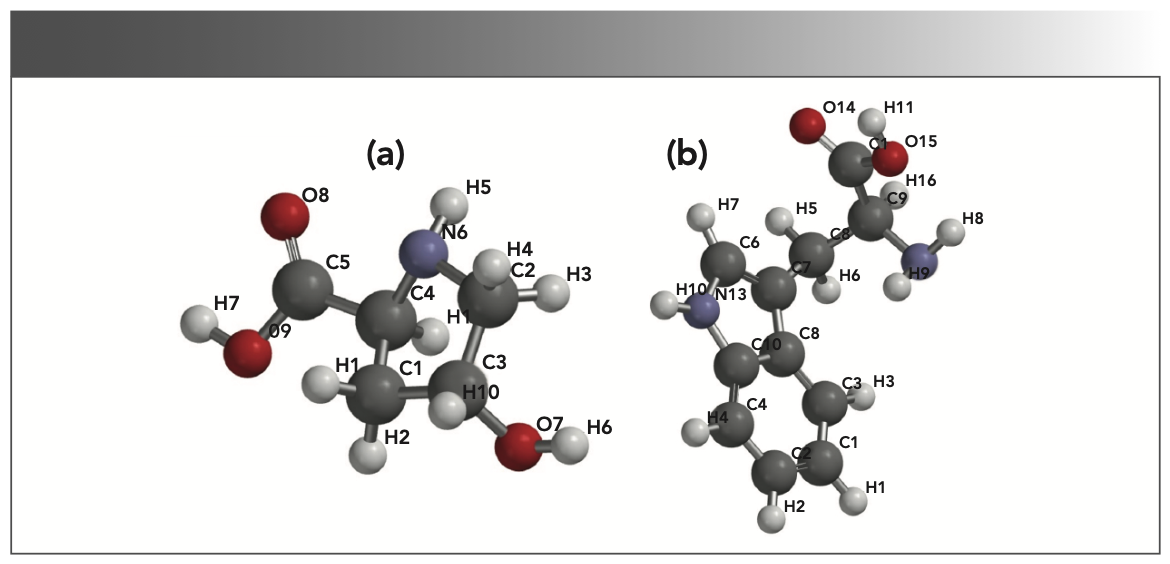
To identify the amino acids, we calculated the Raman spectra for several amino acid molecules, including hydroxyproline (C₅H₉NO₃) and tryptophan (C₁₁H₁₂N₂O₂), the most abundant molecules (28) in the testes specimen. The molecular structures were obtained from the Pubchem database (29) and are shown in Figure 3. Each atom is marked with a number to describe its vibrational mode at a particular frequency.

FIGURE 3: The molecular structures for the (a) hydroxyproline [(2S,4R)-4-hydroxypyrrolidine-2-carboxylic acid] and the (b) tryptophan (2S)-2-amino-3-(1H-indol-3-yl) propanoic acid.

The theoretically calculated spectra for both molecules is shown in Figure 4. The calculations were performed on the pure molecular forms in the gas phase. The calculated spectra show the combination bands (two or more fundamental vibrations, excited simultaneously) and the overtones (vibrational mode excited from the ground state to a state higher than the first excited state) because of the complex geometries of the molecules. Combination bands and overtones generally have lower intensities than the fundamental bands. An actual spectrum from the specimen is the resultant effect of all the molecules present in the specimen. Accordingly, the theoretical model is constructed by computing an average spectrum of both molecules as shown in Figure 5.

FIGURE 4: The calculated Raman spectra for (a) hydroxyproline molecules and (b) tryptophan.

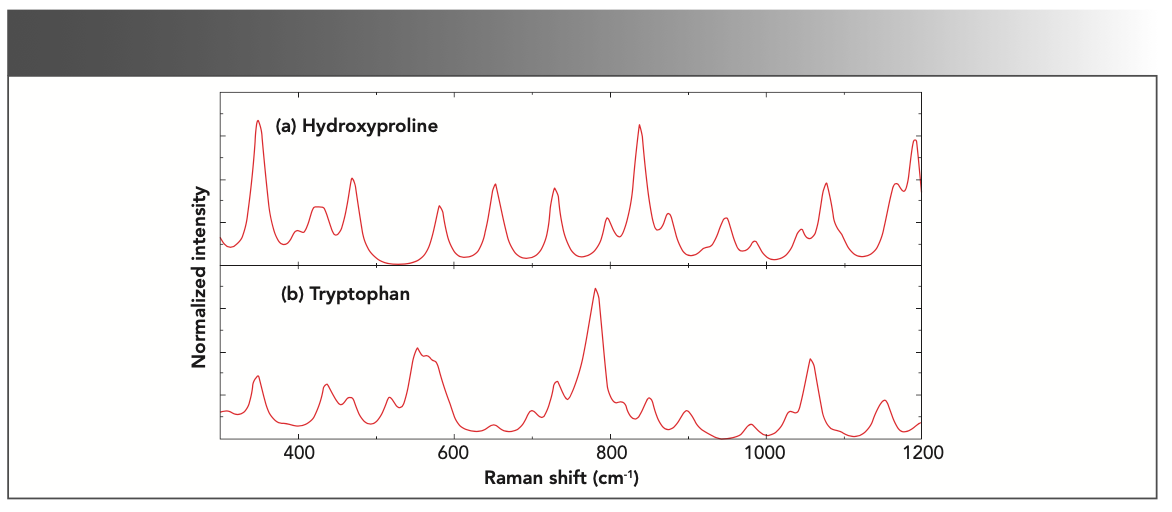
FIGURE 5: The theoretical calculated model Raman spectrum (red solid line) compared to the experimental spectrum (black solid line).

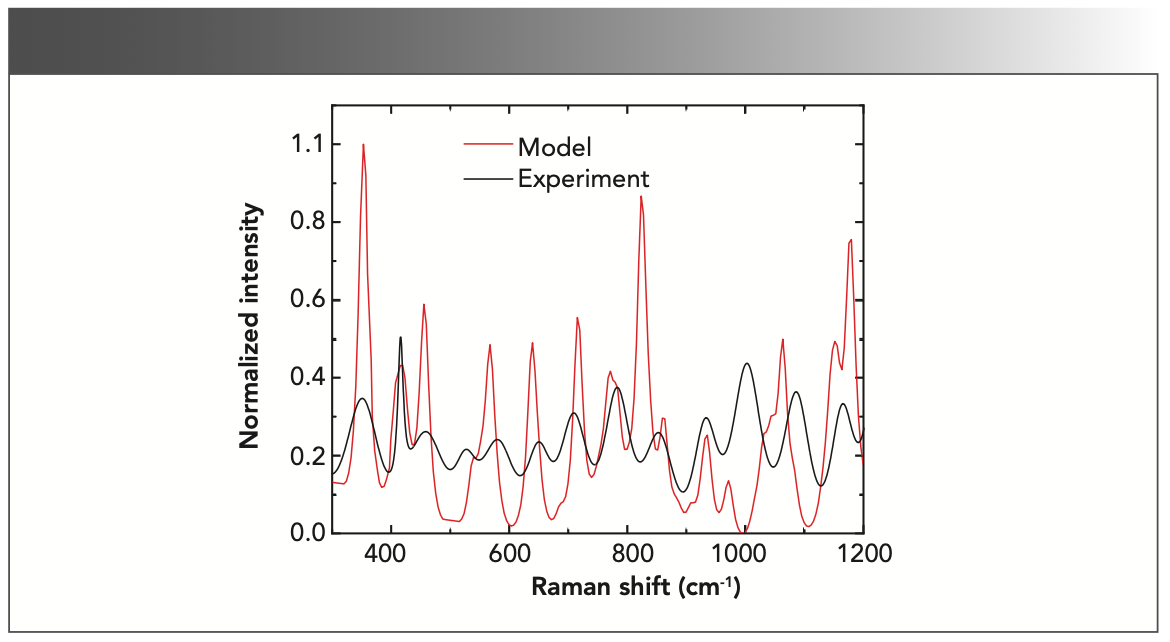
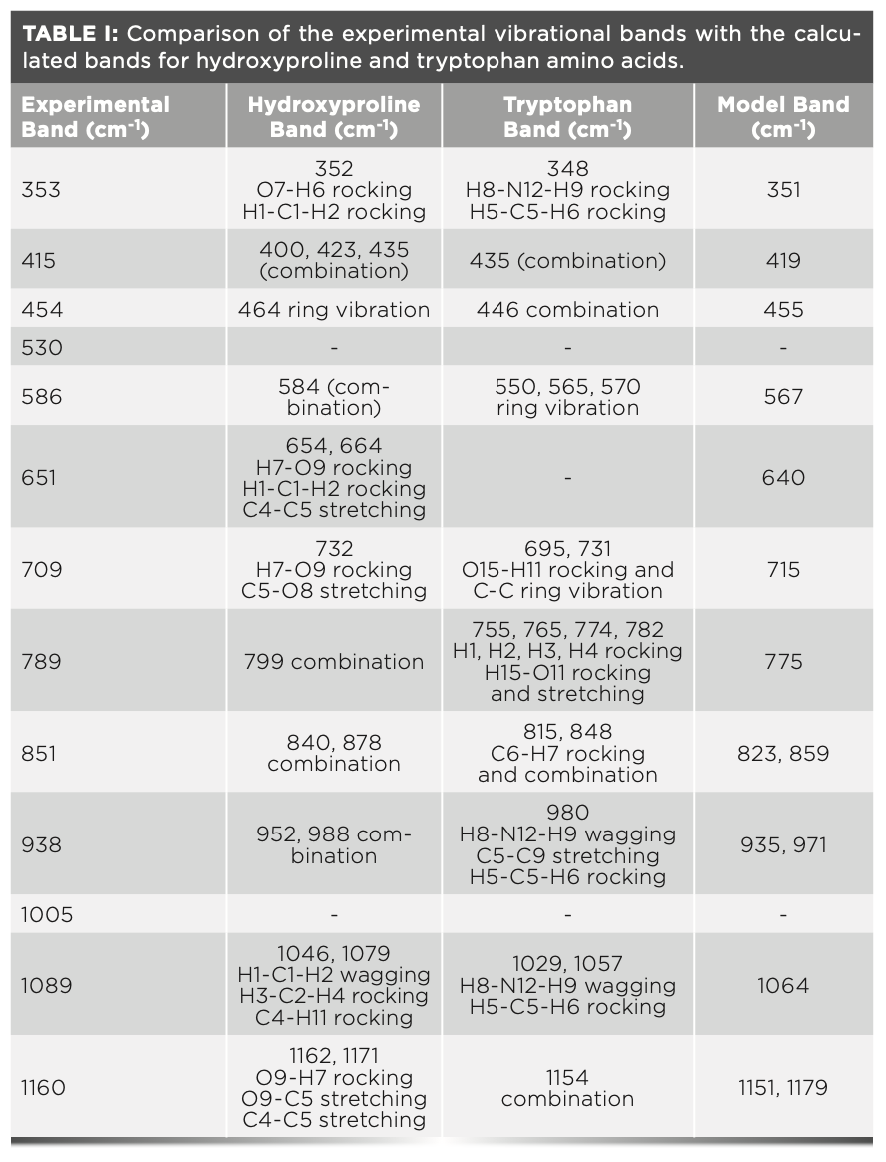
The calculated Raman spectrum shows peaks that are narrower and frequently more intense than the experimental spectrum because the calculation is made on single molecules in the gas phase. The calculations show that the band at 351 cm^-1, which agrees with the experimental spectrum at 353 cm^-1, is a cumulative effect of the rocking vibrational modes of the H-N-H, H-C-H, and C-O-H bonds of tryptophan and the O-H bonds of hydroxyproline. The effects of the O-H vibrations are the strongest among the four bonds. A strong and sharp band at 415 cm^-1 shown in the experimental spectrum is the cumulative effect of the H-C-H and C-O-H vibrations and agrees with the model at 419 cm^-1. The band at 454 cm^-1 in the experiment also agrees with the model, albeit with a more intense peak. The band arises because of C-C ring vibrations of hydroxyproline. A weak band at 530 cm^-1 in the experimental spectrum does not seem to have a counterpart in the model, although the model shows a shoulder at 539 cm^-1. The double C-C bond of tryptophan is responsible for the vibrational band at 586 cm^-1, which is in agreement with the model (567 cm^-1) within the experimental uncertainty. The model band at 640 cm^-1, and the experimental band at 651 cm^-1 are close as well, which are generated by the rocking vibration of the O-H bonds in the hydroxyproline molecule. Next, the model shows a weak shoulder at 687 cm^-1 and a strong peak at 715 cm^-1, the average of which is seen in the experimental at approximately 709 cm^-1. The experimental band at 789 cm also falls close to 775 cm of the model. The band is predominantly the contributions of the rocking and stretching vibrations of the C-C ring of the tryptophan molecule. A strong peak in the model at 823 cm^-1 and 859 cm^-1 was averaged at 840 cm^-1, whereas in the experimental, a peak at 851 cm^-1 was observed. The peaks were the result of the strong C-H vibrations from hydroxyproline and relatively weaker vibrations of C-H bonds in tryptophan. A weak shoulder at 907 cm^-1 followed by a band at 938 cm^-1 in the model was also observed in the experimental at 935 cm^-1. However, a weak peak at 971 cm^-1 in the model was not found in the experimental spectrum. The experimental vibrational band at 1004 cm^-1 was contributed by the breathing modes of C-C rings in proteins (8). Because we did not include proteins in the calculations, we did not observe this vibrational band in the model. The band at 1064 cm^-1 corresponds to the band at 1089 cm^-1 in the experimental spectrum. Finally, the model bands at 1151 cm^-1 and 1179 cm^-1, whose average is 1164 cm^-1, is present in the experimental spectrum at 1160 cm^-1. As expected, these bands represent the C-H bonds vibrations in the hydroxyproline and the tryptophan molecules, respectively. Considering the uncertainty of up to 5% in the experimental measurements, the model was constructed from the single molecules, and the agreement between the experiment and the model is fair. The summary of the mode of vibrations is given in Table I.

It should be noted that our experimental observations of the Raman spectra are significantly different from the previous reports (11,28,30). This is partly because of methodological differences as we used a different source of laser. Previous observations were made by using laser sources of 1064 nm (30), 532 nm (11,28), and 514.5 nm (30), whereas the source wavelength in our experiments was 785 nm. Because our experimental spectra are strongly in agreement with the theoretical model, we trust our observations and interpretations.

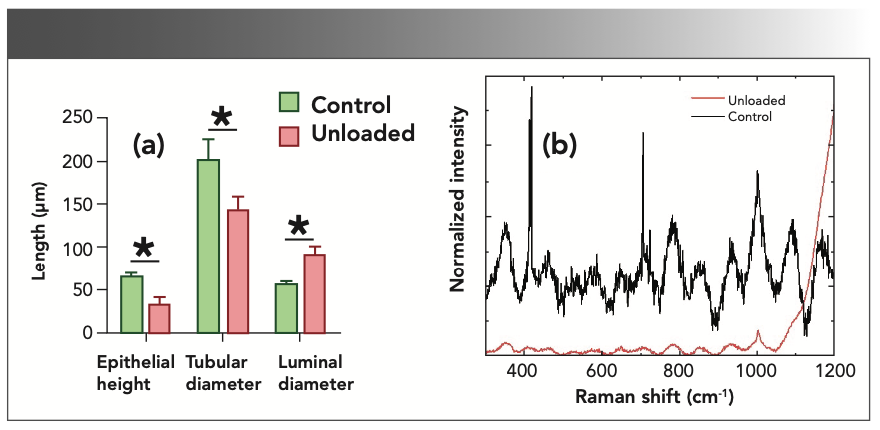
Furthermore, we hypothesized that the histopathological changes in testes, shown in Figure 6a, were accompanied by alterations in the concentration amino acids present in the seminiferous tubules. The atrophy of the tubular epithelia, along with an expansion of the lumen and shrinkage of the tubular diameters (all p < 0.05), was seen clearly in Figure 1. These findings were consistent with similar reports in the testes of HU rats (31) and indicate the vulnerability of testicular architecture to injuries associated with unloading. The cephalic redistribution of fluids seems to be a major trigger of testicular disruption in these cases. Additionally, considering the crosstalk between testes and the musculoskeletal system (32), pathological changes in skeletal muscle and bones can also contribute to testicular dysfunction in HU mice. A disruption of the hypothalamic-pituitary axis was recognized in HU conditions (31), and it can be a potential cause and consequence of testicular pathology in these mice. The Raman spectra from the pre-identified locations from the control and HU testes are shown in Figure 6b. We found a significant drop in the intensity of the spectral peaks of the HU testes. The histological changes were accompanied by generalized depression of the molecular spectra obtained by via Raman spectroscopy (*p < 0.05). This finding provides robust evidence that the concentration of the amino acids has drastically fallen in the HU testes of mice following unloading. It is interesting to note that the peaks above 1000 cm^-1, which are associated with the C-H vibration, have not appeared in the unloaded spectrum, indicating the breakdown of the amino acid molecules. It has been shown previously that the accumulation of the unfolded protein molecules was illustrated by the changes in the spectra range greater than the 1300 cm^-1 in the Raman spectrum (19).

FIGURE 6: (a) The histological changes and (b) the molecular spectra obtained by via Raman spectroscopy *p < 0.05.

Conclusion

The Raman spectra of the hydroxyproline and tryptophan amino acids were calculated by using DFT, and their resultant effect was modeled and compared with the experimental Raman spectra. The theoretical and the experimental spectra agree within the uncertainty which is almost 5% in our experiments. Our model shows that the molecular changes in the seminiferous tubules can be tracked by employing experimental as well as theoretical Raman spectra. Furthermore, our data shows that the HU result in characteristic disruption of normal testicular histology, which is accompanied by a generalized depression of Raman spectra and changes in the intensity or locations of Raman peaks for the hydroxyproline and the tryptophan molecules.

References

(1) S. Palmer, National Research Council (US) Subcommittee on the Tenth Edition of the Recommended Dietary Allowances (National Academies Press, Washington D.C., 10th ed., 1990).

(2) H.J. Butler, L. Ashton, B. Bird, G. Cinque, K. Curtis, J. Dorney, et al, Nat. Protoc. 11, 664 (2016).

(3) A. Rygula, K. Majzner, K.M. Marzec, A. Kaczor, M. Pilarczyk, and M. Baranska, J. Raman Spectrosc. 44, 1061 (2013).

(4) M. Pecul, C. Deillon, A.J. Thorvaldsen, and K. Ruud, J. Raman Spectrosc. 41, 1200 (2010).

(5) A.R. Guerrero and R.F. Aroca, J. Raman Spectrosc. 43, 478 (2012).

(6) S. Bhattacharya, N. Vyas, A.K. Ojha, S. Dasgupta, and A. Roy, J. Raman Spectrosc. 43, 718 (2012).

(7) A.E. Aliaga, I. Osorio-Román, P. Leyton, C. Garrido, J. Cárcamo, C. Caniulef, F. Célis, et al, J. Raman Spectrosc. 40, 164 (2009).

(8) Z. Movasaghi, S. Rehman, and I.U. Rehman, Appl. Spectrosc. Rev. 42, 493 (2007).

(9) R.K. Dukor, in Vibrational Spectroscopy in the Detection of Cancer, J.M. Chalmers and P.R. Griffiths, Eds. (Wiley, Hoboken, NJ, 2006).

(10) L. Zhao, X. Guo, L. Song, Y. Song, G. Dai, and J. Liu, Constr. Build. Mater. 241, (2020).

(11) Y. Liu, Y. Zhu, L. Di, E.C. Osterberg, F. Liu, L. He, et al, Fertil. Steril. 102, 54 (2014).

(12) N. Huang, M. Short, J. Zhao, H. Wang, H. Lui, M. Korbelik, and H. Zeng, Opt. Express 19, 22892 (2011).

(13) N.K. Afseth, V.H. Segtnan, and J.P. Wold, Appl. Spectrosc. 60, 1358 (2006).

(14) N. Huang, M. Short, J. Zhao, H. Wang, H. Lui, M. Korbelik, and H. Zeng, Opt. Express 19, 22892 (2011).

(15) S. Raugei, F.L. Gervasio, and P. Carloni, Phys. Status Solidi Basic Res. 243, 2500 (2006).

(16) S.Z. Fairchild, C.F. Bradshaw, W. Su, and S.K. Guharay, Appl. Spectrosc. 63, 733 (2009).

(17) R.A. Costa, E.S.A. Junior, J.D.A. Bezerra, J.M. Mar, E.S. Lima, M.L.B. Pinheiro, et al, J. Chem. 18, 9627404 (2019).

(18) H. Ren, J.D. Biggs, and S. Mukamel, J. Raman Spectrosc. 44, 544 (2013).

(19) M. Azeem, R. Qaisar, A. Karim, A. Ranade, and A. Elmoselhi, Biochem. Biophys. Reports 25, 100930 (2021).

(20) R. Qaisar, A. Karim, and A. Moslehi, Acta Physiol. 228, e13431 (2020).

(21) M. Maffei, E. Longa, R. Qaisar, V. Agoni, J.‐F. Desaphy, D. Conte Camerino, et al, Acta Physiol. 212, 316 (2014).

(22) E. Bicknell-Brown and K.G. Brown, Biochem. Biophys. Res. Commun. 122, 446 (1984).

(23) W.J. Hehre, A Guide to Molecular Mechanics and Quantum Chemical Calculations (Wavefunction, Inc., Irvine, CA, 2003).

(24) Originlab Corporation, Origin2019b Feature Highlights (2019). https://www.originlab.com/2019b (accessed September 2022).

(25) J.D. Bancroft and C. Layton, Bancroft’s Theory and Practice of Histological Techniques (Elsevier, Amsterdam, The Netherlands, 8th ed., 2019).

(26) A.V. Ranade, Y. Tripathi, R. Rajalakshmi, N.A. Vinodini, R.N. Soubhagya, A.K. Nayanatara, et al, Singapore Med. J. 52, 742 (2011).

(27) Wavefunction Inc., Chemistry at Your Fingertips (2018). https://www.wavefun.com/ (accessed September 2022).

(28) D. Liu, J. Wan, Z. Liu, Z. Zhao, G. Zhang, and Y. Leng, Lasers Med. Sci. 35, 1919 (2020).

(29) S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, et al, Nucleic Acid Res. 47(D1), D1102–D1109 (2019).

(30) P.T.C. Freire, F.M. Barboza, J.A. Lima, F.E.A. Melo, and J.M. Filho, Raman Spectroscopy and Applications (IntechOpen, London, United Kingdom, 2017), p. 201.

(31) A. Moustafa, Reprod. Biol. Endocrinol. 19, 37 (2021).

(32) D. Vaughan, O. Ritvos, R. Mitchell, O. Kretz, M. Lalowski, H. Amthor, D. Chambers, et al, Eur. J. Transl. Myol. 30(1), 8737 (2020).

Muhammad Azeem is with the Department of Applied Physics and Astronomy, College of Sciences, at the University of Sharjah, in Sharjah, United Arab Emirates. Rizwan Qaisar, Asima Karim, Anu Ranade, and Adel Elmoselhi is with the Department of Basic Medical Sciences in the College of Medicine at the University of Sharjah, in Sharjah, United Arab Emirates. Direct correspondence to: mazeem@sharjah.ac.ae ●