The Seven Base Units: Part II

In the previous installment of this column (1), I introduced the concept of base units and discussed several of them. Here, I will complete the discussion of the units themselves and present some associated issues.

But First, A Correction . . .

In the first part of this column (1), I mentioned that the meter used to be based upon a line from the emission spectrum of xenon. I was wrong — it should have been krypton-86, not xenon. Figure 1 shows the correct spectrum, with the ~6057-Å line indicated by arrows. Apologies to my readers for the error, and thanks to Mike Mozil of Lubrizol Corporation for pointing this out to me.

David W. Ball

Now, on with the show . . .

Base Units of Amount and Luminous Intensity

By the early 1800s, it became obvious to scientists that the modern atomic theory was a sound basis for understanding chemical transformations. Work early in that century was focused on establishing the relative weights (actually, masses) of the elements, especially since Lavoisier's 1789 Treatise of Elementary Chemistry established the necessity for the law of conservation of mass in chemical reactions. John Dalton himself proposed a scale of masses in which hydrogen was 1, while J.J. Berzelius, perhaps one of the finest chemical scientists of the first half of the 19th century, proposed a scale with oxygen at 100.

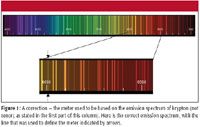
Figure 1

In 1809, Guy-Lussac announced a law of combining volumes, which stated that the volumes of reacting gases and gaseous products had whole number ratios. In 1811, Italian scientist Amedeo Avogadro (Figure 2) became one of the first to differentiate between the terms atom and molecule — previously, the word atom was used for both. In realizing that there was a fundamental chemical difference, Avogadro proposed his own gas law: equal volumes of gases at the same temperature and pressure have the same number of gas species. Ironically, given its central role in science today, Avogadro's proposal was not enthusiastically embraced by the scientific community. It wasn't until the Karlsruhe Congress in 1860, an international (though mostly European) conference of chemists, where fellow Italian chemist Stanislao Cannizzarro pushed Avogadro's ideas, that they finally took hold. The distinction between atoms and molecules became pervasive, and a mass scale with hydrogen as having mass 1 was adopted.

Figure 2

The recognition of the difference between atoms and molecules allowed the modern concept of a balanced chemical reaction to be formulated. Issues such as the law of definite proportions, the law of multiple proportions, the law of conservation of mass, and the law of combining volumes are now obvious — chemical reactions count atoms and molecules, not grams or pounds. In understanding how substances behave and even change, we have to count atoms and molecules.

Problem: Individual atoms and molecules are notoriously tiny. It would take about 360 million, million atoms to make a square with 1 cm to a side and only one atom thick. Real scientists don't deal with individual atoms; they deal with untold thousands and millions of atoms at a time. We would use the units "dozen" or "gross" or "ream" to describe the numbers of atoms or molecules that are present in any one sample, but even 12, 144, and 500 are still too small to be able to express such a quantity easily. We need to use a much, much larger number.

Because of advances in the accuracy of analytical methods, by the late 1800s, oxygen had been chosen as the fundamental basis of relative masses, and it was defined as 16 units. However, with the discovery of isotopes in the 1920s, it was found that oxygen actually existed as a mixture of isotopes. Physicists, using physical rather than chemical methods, used a mass scale based on ¹⁶O, rather than the naturally existing isotopic blend of oxygen. However, it was also found that the exact isotopic blend of oxygen varied, depending upon the source of the oxygen — it varied too much to be used as a standard. Finally, in 1959–1960, international organizations of chemists and physicists agreed to use ¹²C as the standard for relative atomic masses, setting it equal to exactly 12 units.

Although a unit called a mole was first used by Wilhelm Ostwald in 1893, the concept of "gram equivalent" amounts in chemical reactions was relatively well known. However, in 1971, the 14th Conférence générale des poids et mesures (CGPM, the General Conference on Weights and Measures) formalized it: the unit mole, abbreviated mol, is equal to the number of fundamental chemical entities that appear in exactly 0.012 kg of carbon-12. While similar in theory to a dozen, a mole of atoms or molecules actually has a mass that is easy to manipulate in the laboratory, kitchen, basement, garage, or wherever someone performs experiments. Careful experiments allow us to determine how many entities this is; the currently accepted value is that there are 6.022 136 7 x 10²³ (602 213 670 000 000 000 000 000) things in a mole of things. That's a bit more than 12 in a dozen . . .

Luminous intensity is the name given to the quantity of power given off by a light source per solid angle unit. The solid angle unit is the steradian; a unit sphere has 4π steradians of solid angle, or 129 600/π square degrees of solid angle.

Luminous intensity was one of the last units to be standardized. In the early 1900s, the U.S., France, and the U.K. agreed on the international candle as the unit of luminous intensity. It was defined as the amount of light given off by a one-sixth pound spermaceti candle burning at a rate of 120 grains per hour (where 1 grain = 1/7000th of a pound), or about 7.78 g/h. In 1937, the international candle was defined in terms of a blackbody at the freezing point of platinum (1768 °C, or 2041 K). One square centimeter of blackbody at that temperature had a luminous intensity of 58.9 international candles. In 1946, the luminous intensity of the square centimeter was revalued to 60 "new candles," ever so slightly changing the size of the candle unit. In 1948, the word candela (abbreviation "cd") was adopted as the new name for the unit.

In 1979, the 16th CGPM adopted the current definition. One candela, they decided, would be equal to 1/683rd of a watt per steradian of light having a frequency of 5.40 x 10¹⁴ s^-1 . Light of this frequency has a wavelength of about 555.2 nm and is the color that the human eye is most sensitive to. The fraction 1/683 seems unusual (indeed, 683 is a prime number). It was apparently used in order to make the new candela unit as close to the previous definition as possible. This definition of a candela represents about 4.092 x 10¹⁵ photons of green-colored light per second.

To get an idea of how bright this is, a 100-W incandescent light bulb, a common bulb in pre–compact fluorescent days, has a brightness of about 120–135 cd. Bright sunlight is about 10,000 cd per square meter, while moonlight is only about 0.1 cd/m² .

The candela is unusual in that it is actually defined in terms of a derived unit (watts; see below), while all other base units are defined in terms of a specific number of things or phenomena. Nonetheless, a candela is a base unit of the SI system.

Derived Units

Using the seven base units as the starting point, other units can be constructed; these are called derived units. Derived units are constructed by multiplying or dividing the base units. Occasionally, the derived unit itself is given a name, giving some people the misleading impression that they are more fundamental units than they actually are. For example, to describe a volume, we can describe it ideally as being a length times a width times a height; therefore, the basic unit for volume is m x m x m, or m³. This derived unit is actually too large to be useful for many purposes, so we use 1/1000 of this volume, which we rename the liter (abbreviation L). Units for speed include meters per second, which involves the division of one unit into another: m/s. Acceleration is m/s² ; force is kg·m/s² (which is renamed a newton, abbreviated N); energy is kg·m² /s² (which equals N·m and is renamed the joule); and power is kg·m² /s³ , which is equal to a J/s and is renamed a watt (abbreviation W).

Most units are derived units. The International Union of Pure and Applied Chemistry (IUPAC) publishes Quantities, Units, and Symbols in Physical Chemistry, which details many defined units (2). Chapter 2 of the book lists hundreds of types of quantities, all of whose units are either one of the seven base units or some combination thereof.

Prefixes

In many cases, the base unit or a derived unit might not have the right size to succinctly describe a quantity — one example was given above, when using the cubic meter to describe volume. Although a system of units based upon decimalization was proposed as early as 1586 (by Flemish mathematician Simon Stevin), the first systematic proposal for a decimalization of units was made in 1875 by the Convention du Mètre, mentioned in the previous column. As part of the metric system (as it was called back then), a series of combinatorial prefixes and associated abbreviations was adopted to modify the fundamental unit (whether base or derived) to a more appropriate size. For example, consider the base unit kilogram. The kilogram is based upon the fundamental unit the gram, and has been modified by the prefix kilo-. The prefix kilo- is defined as "1000 times," meaning that it is 1000 times the size of the gram. Some prefixes represent multiples of the fundamental unit, while others represent fractions of the original unit — but all prefixes imply a certain power of 10, so all prefixes have the effect of moving a decimal point to the right or left of 1.

Each prefix also has an associated abbreviation that can be combined with the abbreviation of the fundamental unit to give the abbreviation of the modified unit. The abbreviation for kilo- is k; when combined with the abbreviation for the gram, g, the abbreviation for kilogram is produced: kg. Table I gives the current list of approved units that are part of the SI system.

Table: Unit prefixes, abbreviations, and multiplicative values.

There are some conventions when using the prefixes and their abbreviations. Only one prefix is used at a time on a unit. If more than one multiplier is needed, use a different prefix. So, instead of saying "kilokilogram," say megagram. Note that the case of the abbreviation is important: if you use ps instead of Ps, you are implying picosecond instead of petasecond — both useful units, but hardly interchangeable! There is no space between the prefix and the fundamental unit, either when spelled out or when abbreviated. Hence, a femtosecond is not spelled "femto second," nor is it abbreviated "f s." Finally, note that some of the abbreviations are also abbreviations of units. The most obvious example is the use of the letter m to represent meter as well as the prefix milli-. People using these abbreviations need to understand what they represent based upon their usage — "mm" means "millimeter," while "ms" means "millisecond, not "meter second." (If, for any reason, a meter second is the appropriate unit, it would be written as "m s", with spaces between the unit, or "m x s" or "m·s," with the multiplication operation shown explicitly.) These conventions are neither capricious nor unnecessary — they are crucial to being able to communicate quantities and their units properly.

The prefixes in Table I are getting more and more use as society progresses. Already we are measuring time periods on the order of attoseconds (10^-18 s) and computer memory in terms of terabytes and petabytes (10¹² and 10¹⁵ bytes, respectively). I predict we will be seeing more zepto-, zetta-, yocto-, and yotta-based units in the years to come.*

Notes

*Although these last few prefixes sound like random syllables, they are actually derived from the Latin septum and the Greek octo, respectively. This is because they represent 1000 raised to the seventh or eighth power, either as a multiplicative or as a divisive factor. They do remind this author of the Marx brothers, though — can a harposecond or grouchogram be far behind? And once we're finished with the Marx brothers, we can always use the Three Stooges as inspiration; curlycandela or moemeter, anyone?

David W. Ball is a professor of chemistry at Cleveland State University in Ohio. Many of his "Baseline" columns have been reprinted in book form by SPIE Press as The Basics of Spectroscopy, available through the SPIE Web Bookstore at www.spie.org. His book Field Guide to Spectroscopy was published in May 2006 and is available from SPIE Press. He can be reached at d.ball@csuohio.edu his website is academic.csuohio.edu/ball.

References

(1) D.W. Ball, Spectroscopy 24(1), 22–28 2009.

(2) I. Mills et al., Quantities, Units, and Symbols in Physical Chemistry, 2nd ed. (Blackwell Science, Oxford, 1993).